※当記事は、下記記事からの続きとなります。
【波の解析編】
CONTENTS

昼食の後、僕たちは雑談に花を咲かせていた。
ミア:「ねぇシエル、港に船が止まっているとしたら、どんな船を想像する?
あと、その船には簡単に乗船できる?」
シエルちゃんは面倒くさそうに答える。
シエル:「何その質問?何かの心理テスト?」
僕:「結構有名なやつだよ。
因みに、ミアと僕は全く同じ答えで、簡単に乗り込める、小さい漁船を想像したんだ。」
シエル:「ふ~ん。
海賊船かな…でっかいヤツ。
セキュリティは厳しくはないけど、私が認めない限り乗せることはない。」
ミアは少し表情を曇らせて言う。
ミア:「なるほど…じゃぁ、その船の中に動物が乗っているとしたら、何が乗っている?」
シエル:「次は動物?
うーん、パッと思い浮かぶのはライオンだね!
なんで居るのかはわからないけど...。」
ミア:「じゃぁ答えを言うね。
このテストでわかるのは、
船の大きさは、野心の大きさで、船が大きければ大きいほど野心も大きいです。
船の乗り易さは、その人の心が開放的かどうかを表していて、乗り易いなら開放的で、乗りにくいなら閉鎖的です。
中の動物は人生の満足度を表していて、小さい動物を想像した人は満足度が高く、大型で凶暴な動物を想像した人は爆発寸前です!
シエル...悩みは抱え込まないで相談すると楽になるよ。」
シエルちゃんは僕たちから視線を逸らして言う。
シエル:「2人に相談することなんてないよ!
...ところで、2人はどんな動物を想像したのかな?」
僕:「これも、全く同じで猫だったんだ。
長いこと一緒に居ると、考え方も似るものだね。」
シエル:「そうですか!2人とも今が幸せの絶頂とは、羨ましい限りだよ!」
僕:「ハハハ、そうだね。」
そう...今が幸せの絶頂だ。
だから、僕の進む先にあるのは、もう下り坂だけだ。
シエルちゃんは一瞬だけスマホを光らせて時間を確認する。
シエル:「おっと、休憩はこの辺にして、そろそろ話を進めないか?」
僕:「そうだね。
そういえばシエルちゃん、咳止まったね。
ご飯食べたら風邪の症状が軽くなることってあるけど、それかな?」
シエル:「確かに、今気づいたぞ!
...よし、始めようか!」

文系投資家の修行~三角関数は投資家を救うのか?~【後編】

弧度法
シエル:「よし、始めようか!
これから『波の解析』に重要な正弦波について詳しく見ていくが…
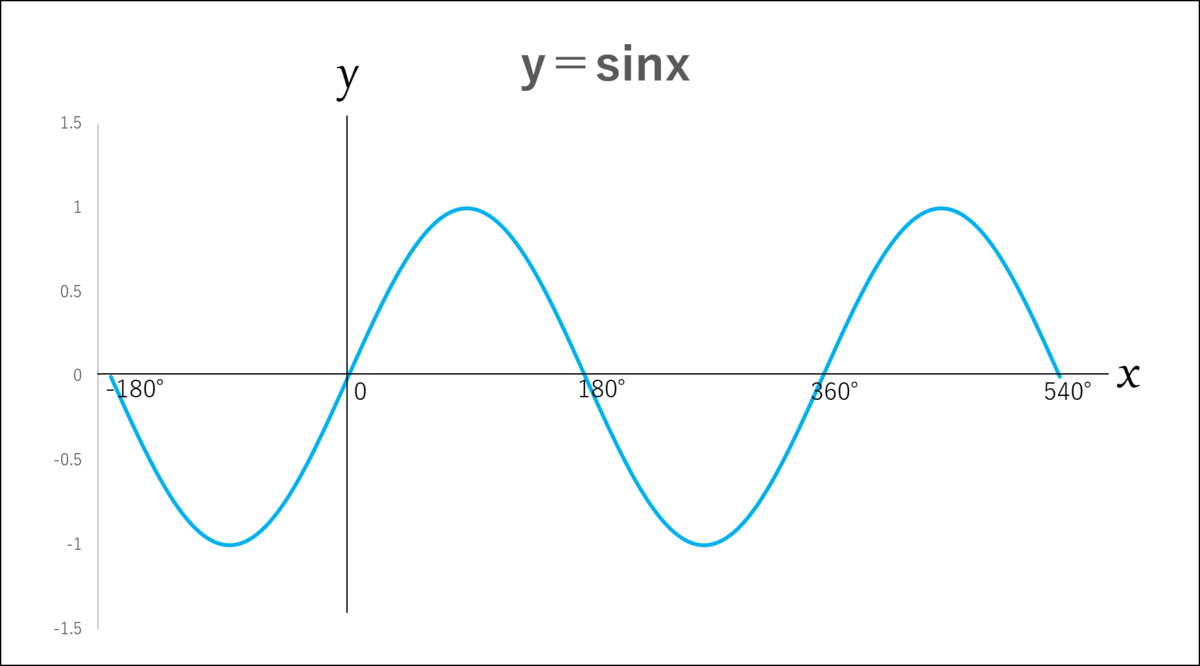
その前に基礎知識として、これから教える2つのことを頭に入れておいてほしい。
一つ目は『弧度法』だ。」
ミア:「コドホウ?」
僕:「そっか、前にこの話をしていたときはミアは熟睡していたね。」
ミア:「・・・」
シエル:「弧度法は意味が理解できないとつまづくことが多い…まさに文系泣かせの表記法だ。
でもルールがわかれば簡単だ。
通常の度数表記では360°と書くものを、弧度法では2πと書く…たったこれだけだ。
つまり、360°=2π…これより、
あらゆる角度に『360°分の2π』を掛ければ、その角度を弧度法で表すことができる。
たとえば、180°は
180°×2π/360°=π…となる!
じゃぁミアちゃん、60°を弧度法で表したらどうなる?」
ミア:「360°分の2πを掛ければいいのよね?
え~っと…
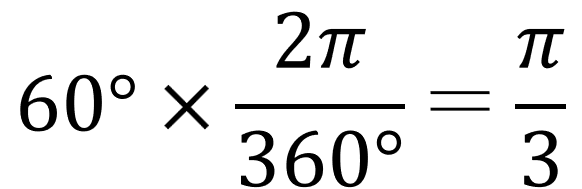
わかったよ!
60°は『3分のπ』!」
シエル:「いいねぇ~。
じゃぁ270°は?」
ミア:「これも同じようにして…
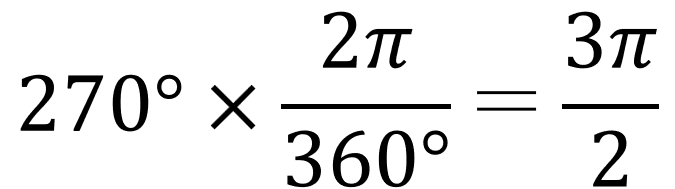
270°は『2分の3π』!」
シエル:「エクセレント!
ミアちゃんは並みの高校生より冴えてるよ!」
ミア:「フフッ…楽勝♪」
シエルちゃんはミアをおだてるのが上手いな…。
シエル:「次はミクサの番。
『4分の3π』は何度?」
僕:「2π/360°の逆数を掛ければいいね。
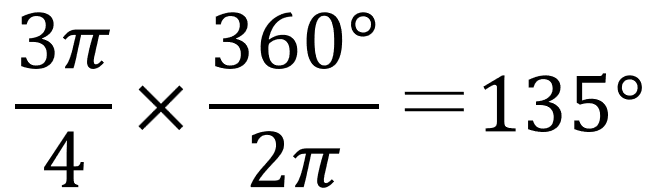
4分の3πは135°のことだね。」
シエル:「よし。2人とも弧度法については理解できたね。
今後は、度数表記をやめて弧度法を使っていくよ。
では基礎知識の二つ目…関数の平行移動だ。
座標平面上に点Aがある。
点Aの座標は(x,y)だ。
この点Aをx軸方向に1、y軸方向に1動かしたところを点Bとしよう。
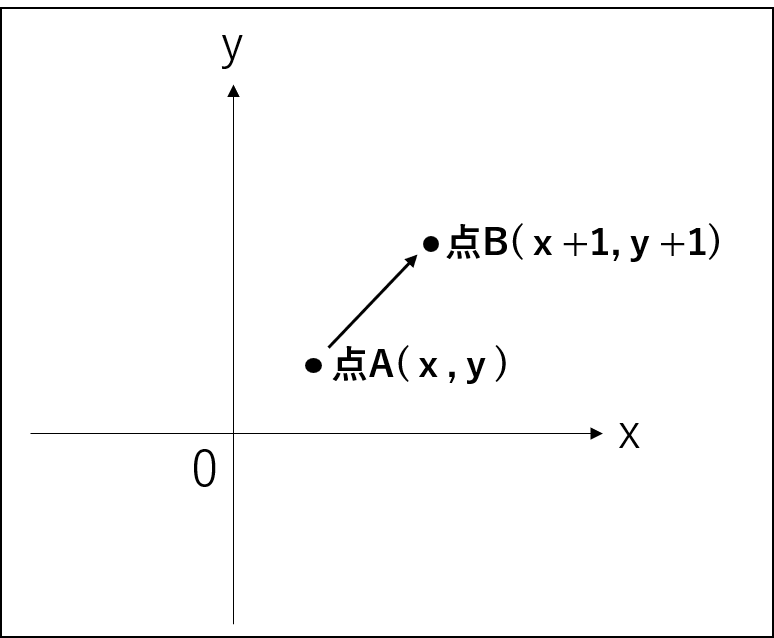
この時、点Aから見た点Bの座標は
(x+1,y+1)だが、同時に点Bから点Aを見ると、
点Aの座標は(x-1,y-1)となる。
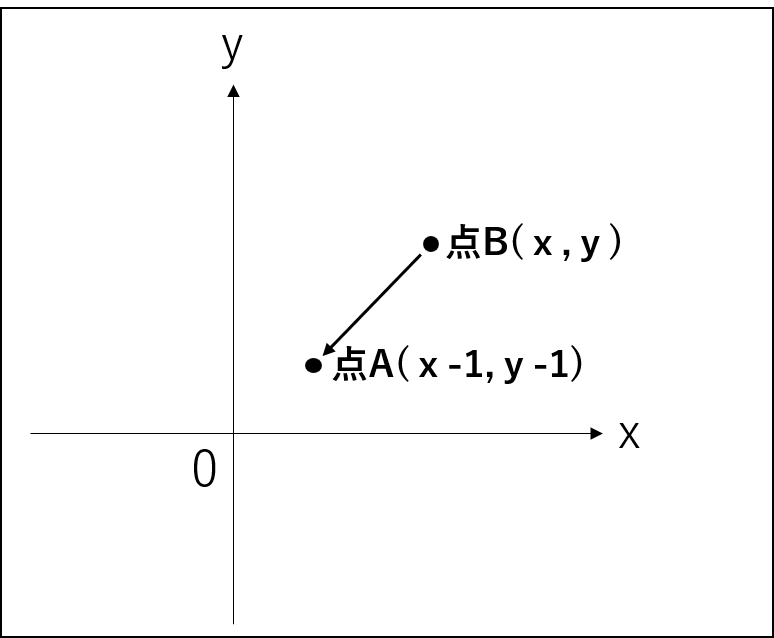
関数の平行移動では、点Bから見た点Aのことを考える。
つまり、関数y=xをx軸方向にP、y軸方向にq平行移動させた関数は、
y-q=x-p⇒y=(x-p)+qとなる。
試しに、二次関数y=x²をx軸方向に1、y軸方向に1動かしてみよう。」
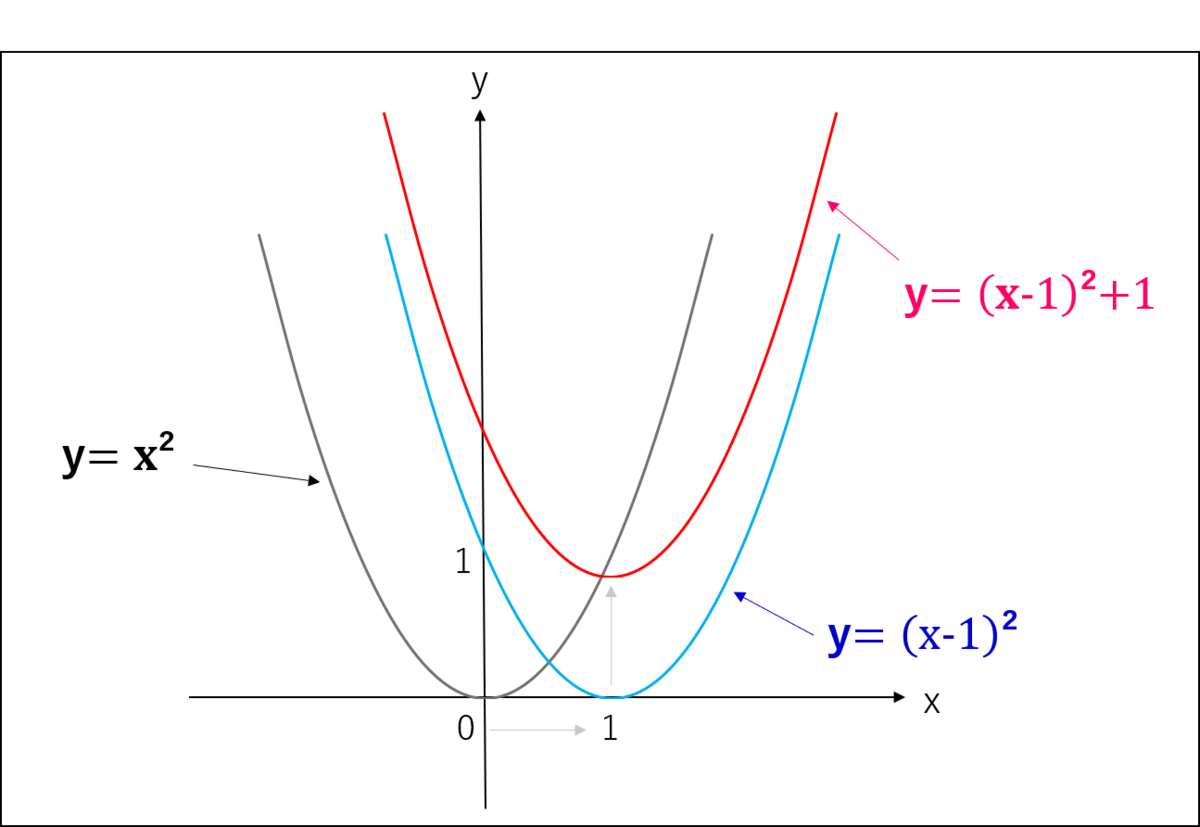
※上図はイメージです。
ミア:「なんとなく、わかるような…わからないような?」
シエル:「基本的に関数のグラフは、式を
『y=a(x-p)+q』の形に直してから描く。
二次関数の場合も同様に、
![]()
という式を
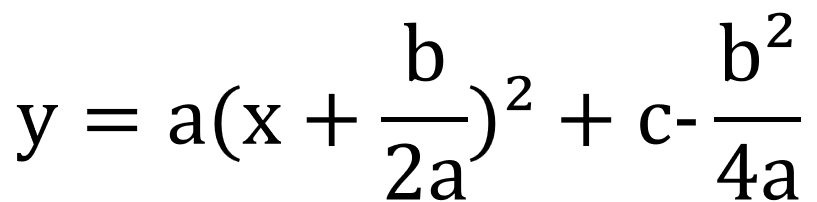
の形に変形させてから描く。
因みにこれは平方完成と呼ばれる手法だが、覚えておいて損はないぞ!」
僕:「平方完成はさておき…
要は、x軸側の符号は逆になるんだね。
やや直感に反するけど…なんとかなりそうだよ。」
シエル:「では、本題に入るとしよう!」

正弦波の変形
シエル:「では、本題に入るとしよう。
これまで、正弦波のことを
『y=sinx』としてきたけど、ここからは
『f(x)=sinx』と改める!
度数表記もやめて弧度法で正弦波を描き直すよ。」
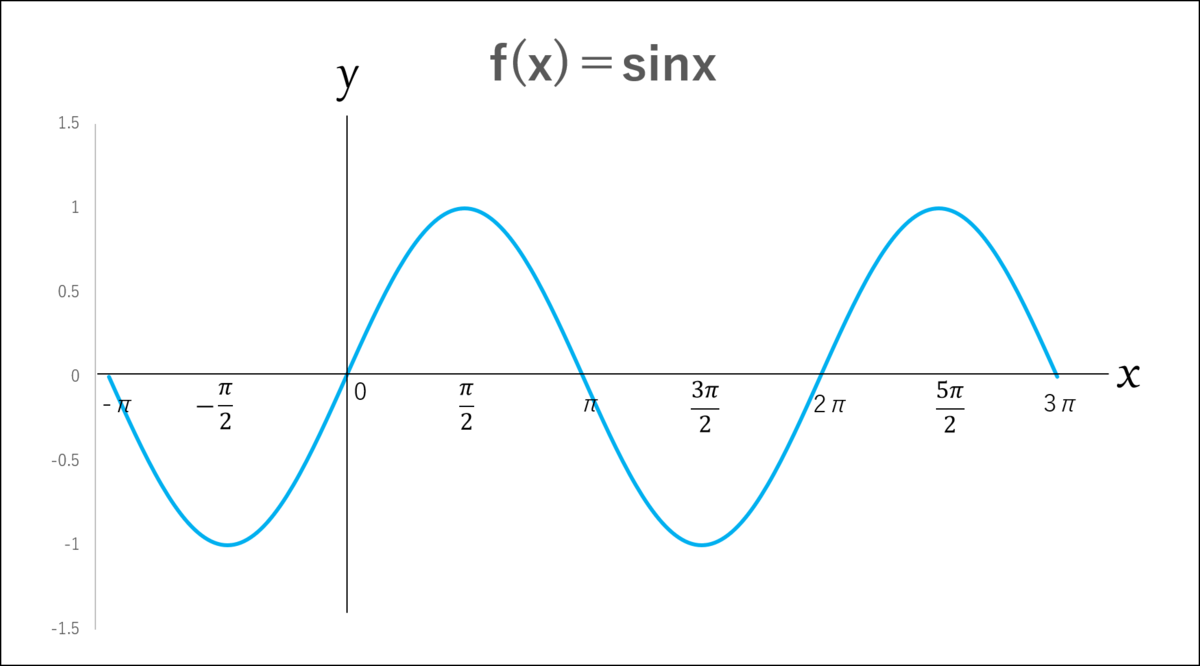
ミア:「うん…ここまではOKだよ。」
シエル:「じゃぁ、このグラフを
x軸方向に-π/2…つまりマイナス90°平行移動させると、このグラフはどうなると思う?」
ミア:「う~んと…
0のところがマイナス2分のπに来るんだよね?
えーと…こんな感じ?」
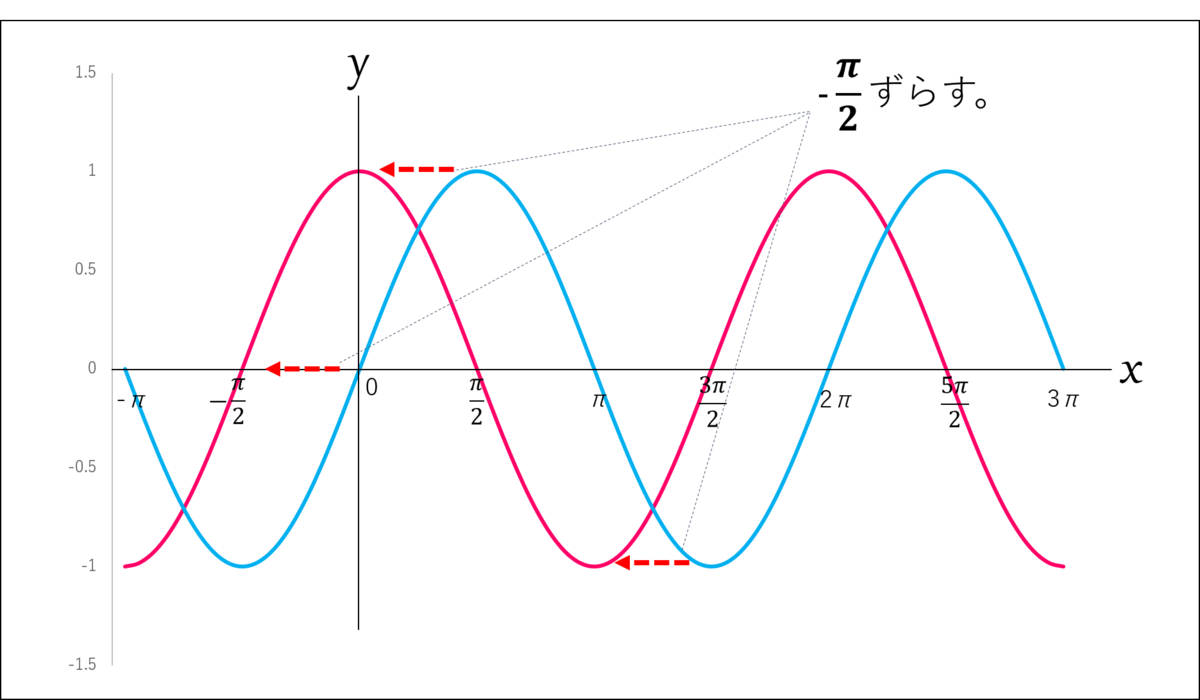
僕:「すごいなミア!僕はこういうのちょっと苦手だな…。」
シエル:「流石ミアちゃん!理系の素質があるね!」
ミアは少し照れた顔で言う。
ミア:「そうかな~?シエル、夜ご飯も食べて帰る?」
シエル:「ホントか!?ゴチになる!」
『生活費カツカツ』…じゃなかったのか?
シエル:「何度も言うけど、関数のグラフは式を
y=a(x-p)+qの形に直して描く。
もちろん、これは三角関数も例外ではないよ。
先ほどの、
x軸方向に-π/2動かした三角関数の式を次のように書く。」
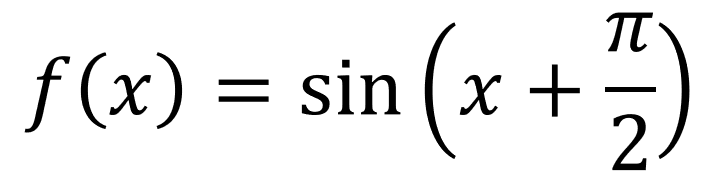
シエル:「あと、気付いてるかもしれないけど…
この式のグラフは
余弦派『f(x)=cosx』と同じものだよ。
つまり余弦派も正弦波の一部だったということだね。
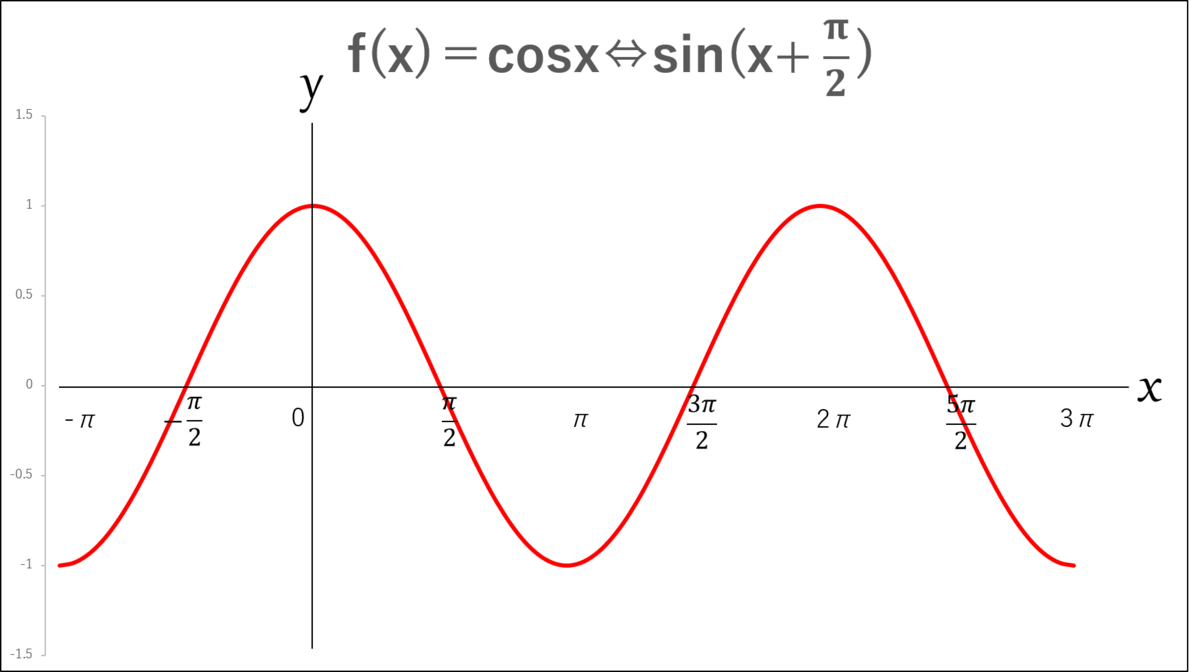
僕:「なるほど…他にも、いろいろと変形ができそうだね?」
シエル:「もちろん、これだけじゃないよ♪
次は振り幅を2倍に増幅させてみよう…式は、
『f⒳=2sinx』だ。」
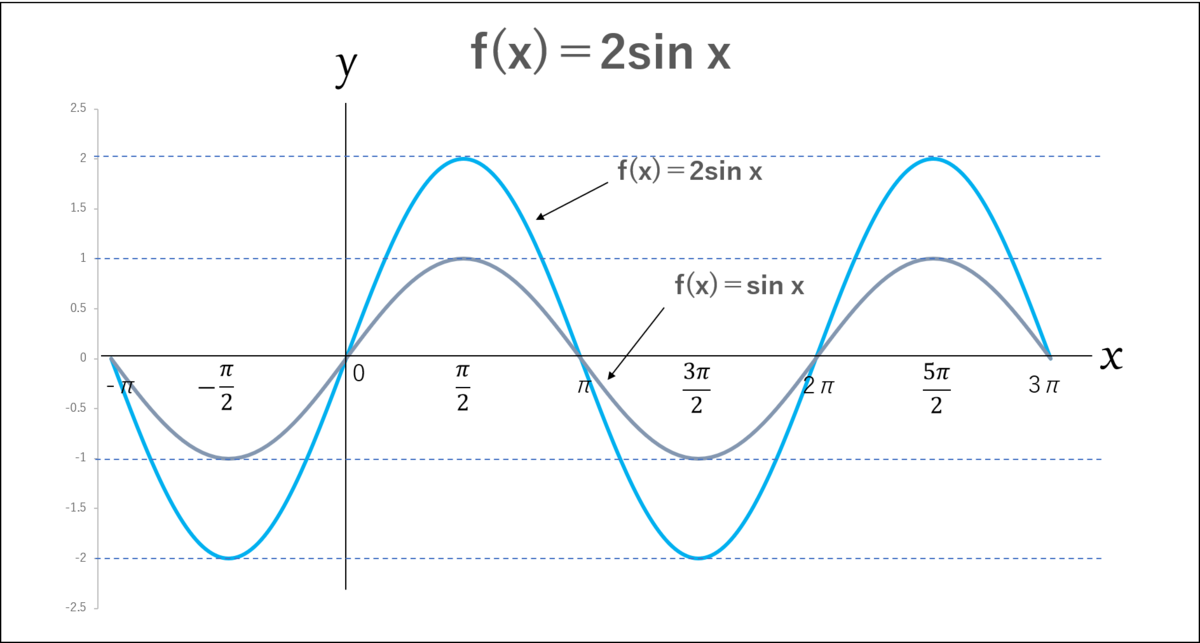
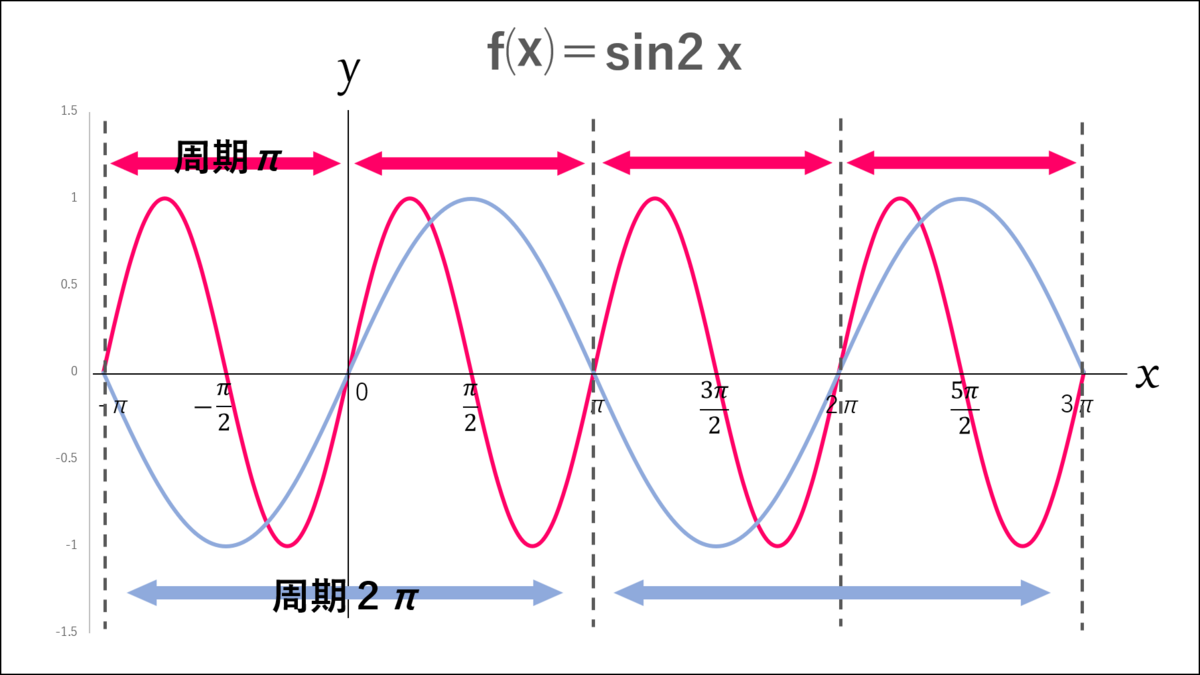
シエル:「最後に周期をイジる。
これまで見てきた正弦波はどれも2πで一周する関数…
つまり周期2πの周期関数だった。
じゃぁ試しに『f⒳=sinx』の周期を2πから半分のπにしてみようか。
式は『f⒳=sin2x』だ。」
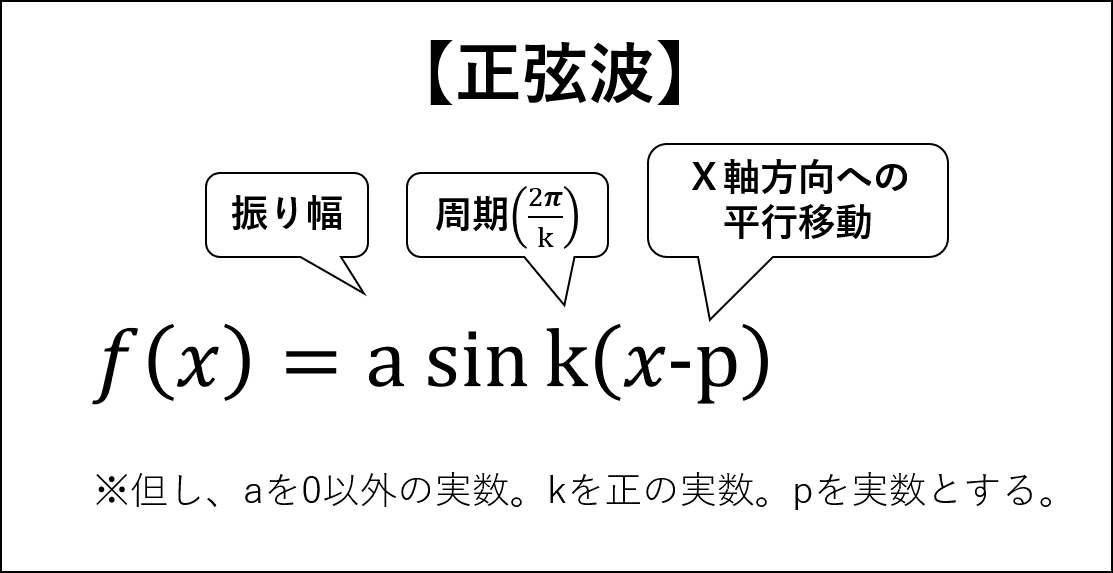
シエル:「まとめるよ!
多くの文系人は正弦波のことを
『y=sinx』の式で認識しているけど…
正弦波の本当の姿はこのような式になる。」
僕・ミア「かっこいい…」
僕は、ミアが同じ言葉を発したことに少し驚いた。
僕:「ミアは、この式のどこがかっこいいと思ったの?」
ミア:「だってこの式、一つも数字が入ってないんだよ!
それに、横一列に並んでいて…すごいシンプルだよね!」
僕:「うん、そうだね!
これを使って波を解析するのか…面白そうだな。」
シエル:「これで満足しちゃだめだよ!
波の解析ではさらにカッコイイ式が登場するからね♪
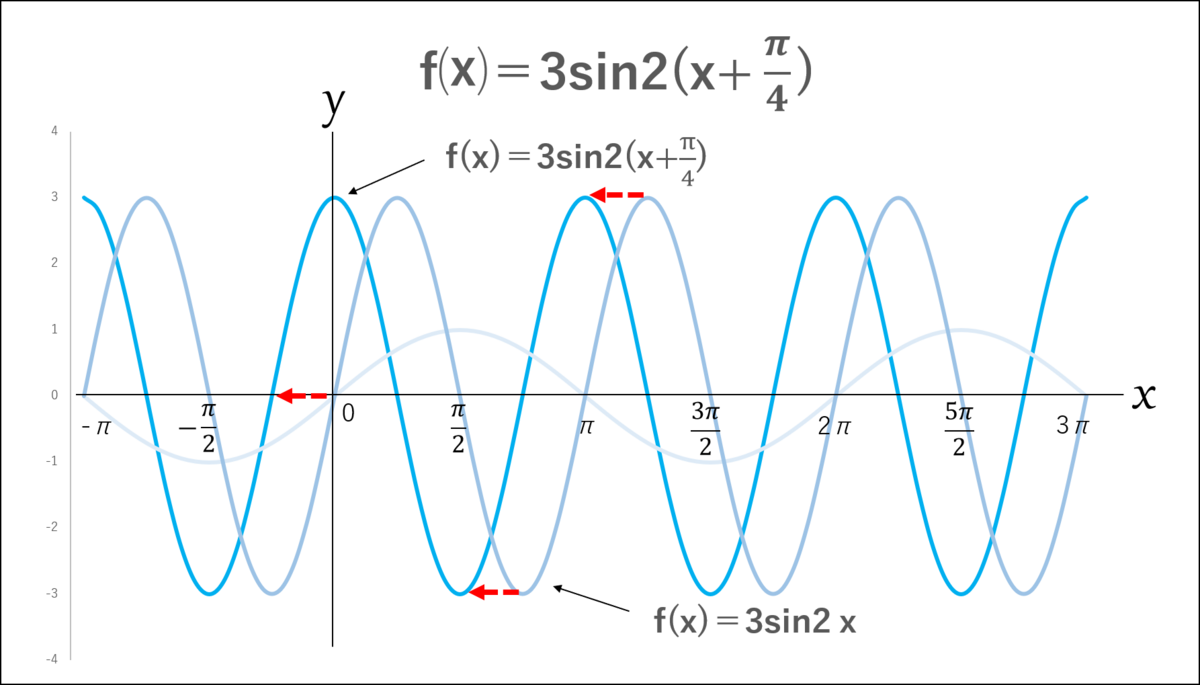
じゃぁ、正弦波の式を使って、
振り幅が3で周期πの正弦波を、x軸方向にーπ/4だけ平行移動させたグラフを描いてみよう!」

咲いたコスモス、コスモス咲いた。
シエル:「変形させた正弦波を無数に組み合わせていくことで、あらゆる波の形を合成して作り出すことができる。
その波が、どんな波の組み合わせでできているのかを調べるのが波の解析だ!
ただ…そのためには、文系人には少しキツイ試練を乗り越えてもらう必要がある…。
加法定理だ。」
僕:「・・・避けては通れないの?」
シエル:「無理だ。受け入れろ。」
ミア:「加法定理…なんだっけ?」
僕:「いっぱい公式が出てくるやつ。」
シエル:「加法定理は文系人中心に敬遠されることが多い。
だが、そこまで難しく考える必要はないよ。
たった3つの公式さえ知っていれば、三角関数の公式を全て導き出すことができるんだ。
ミアちゃん、sin(90°)はsin(30°+60°)で導けるけど…計算してみてくれる?」
ミア:「sin90°=1…わざわざ計算しなくてもわかるけど…
sin30°もsin60°も、今日の話で出てきたよね。
え~と…
sin30°は1/2で、sin60°は√3/2だから…
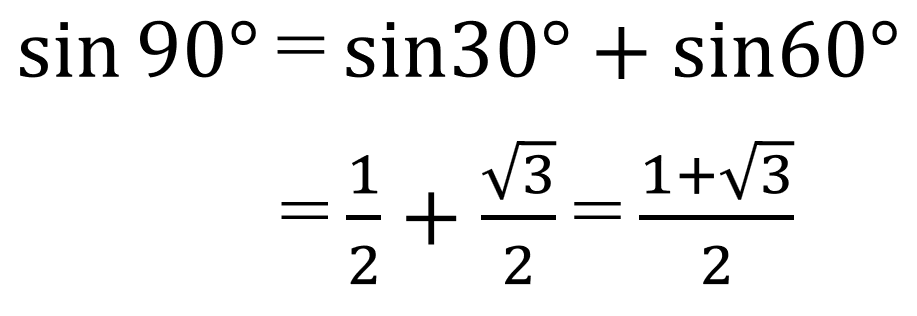
・・・あれ?」
シエル:「そう計算できれば簡単なんだけど、残念なことにそうじゃない。
これを計算できるようにするのが加法定理だよ。
この2つの公式を、
『咲いたコスモス、コスモス咲いた』で丸暗記しろ!」

シエル:「最初は拒絶反応で苦しいだろうが…
数学の基本は『習うより慣れろ』だ!
とりあえず、sin90°をこの公式に当てはめて計算してみようか!」
ミア:「なんでただの足し算がこんな複雑になるのよ…
この式に数字を当てはめればいいのね?」
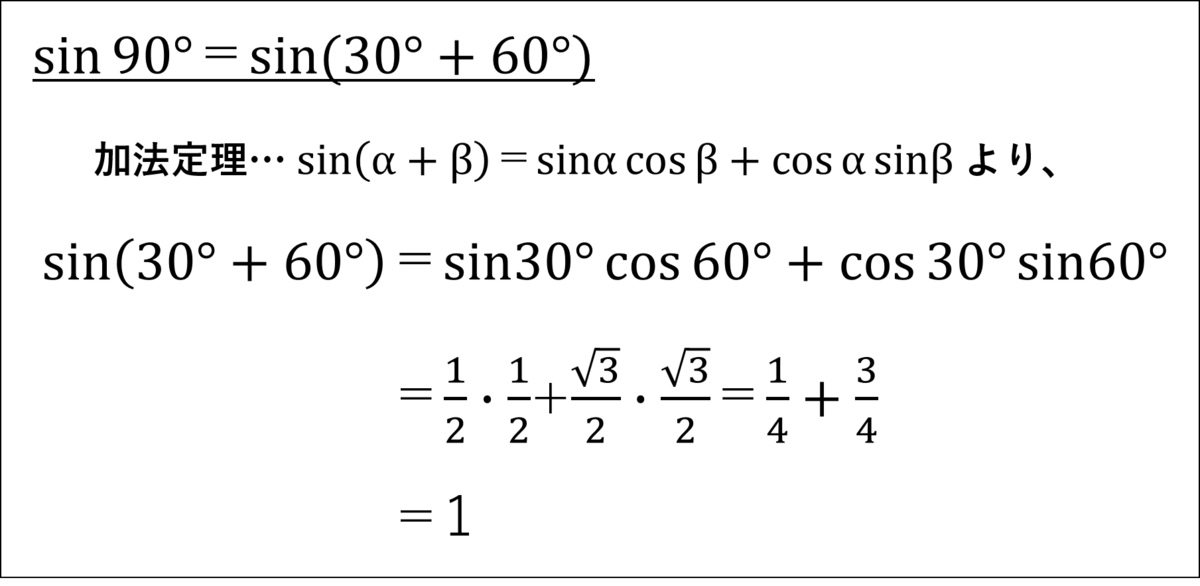
ミア:「できたけど…これすごい疲れる…。」
僕:「まるでパズルみたいだね。
ところで、(α-β)の場合はどうするのかな?」
シエル:「βをーβに置き換えればいいだけだよ。
図を見てもらえばわかると思うけど…θの値をマイナスにした場合、
y軸に値するsinθの値だけが符号がマイナスになり、cosθの値は変化しない。
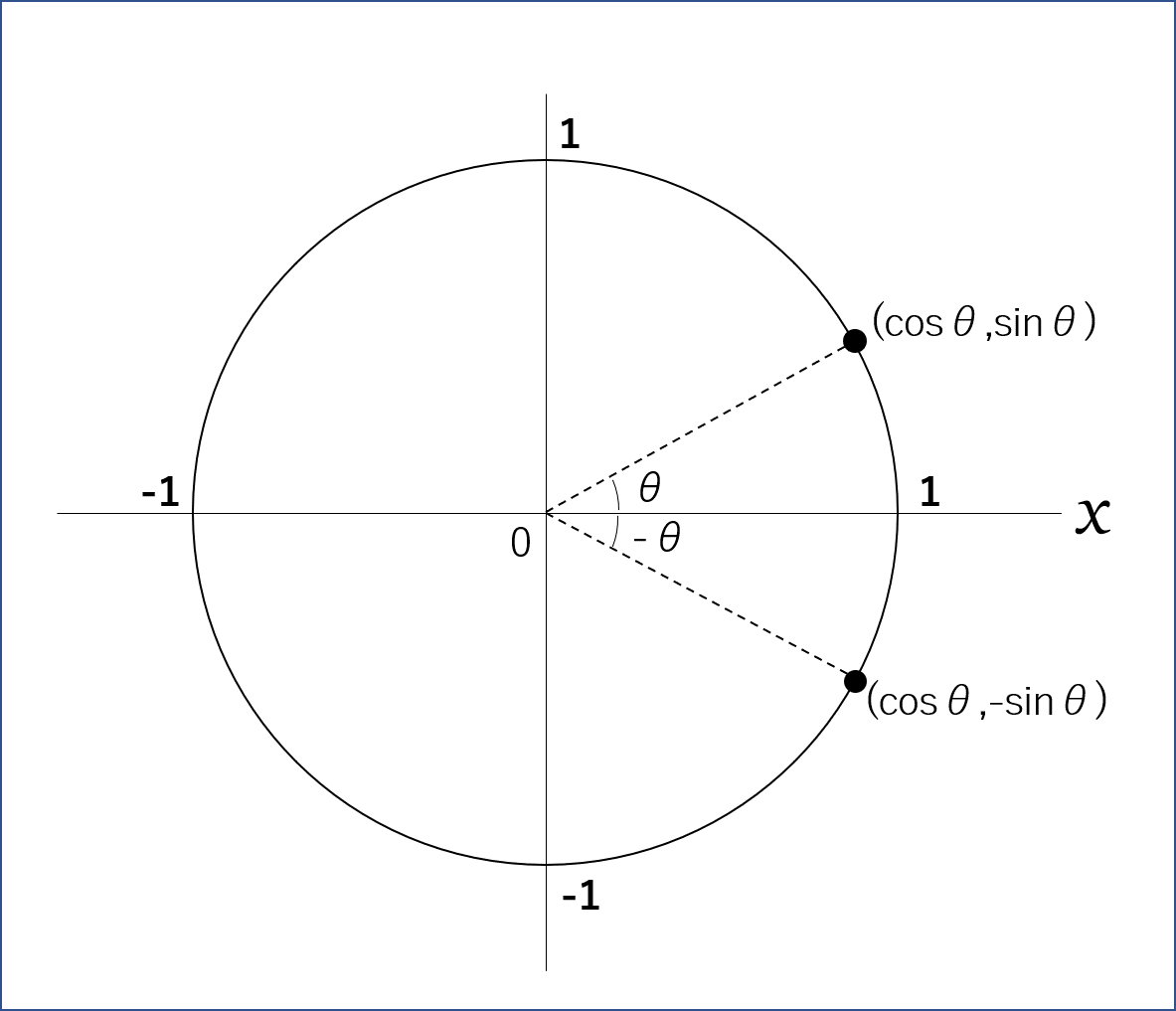
つまり、『sin(-β)』は『ーsinβ』となり、『cos(-β)』は『cosβ』となる。」
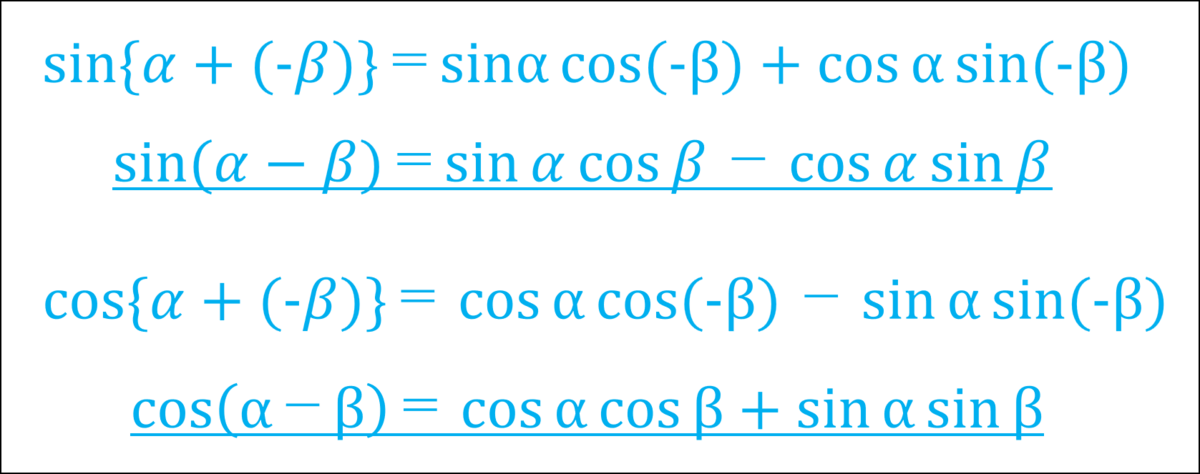
シエル:「これら加法定理の公式を使えば、さまざまな三角関数の計算公式を導くことができる。
やることは簡単で、これら式を足したり引いたりすればいい。
まずは『sinα・cosβ』を導こう。」
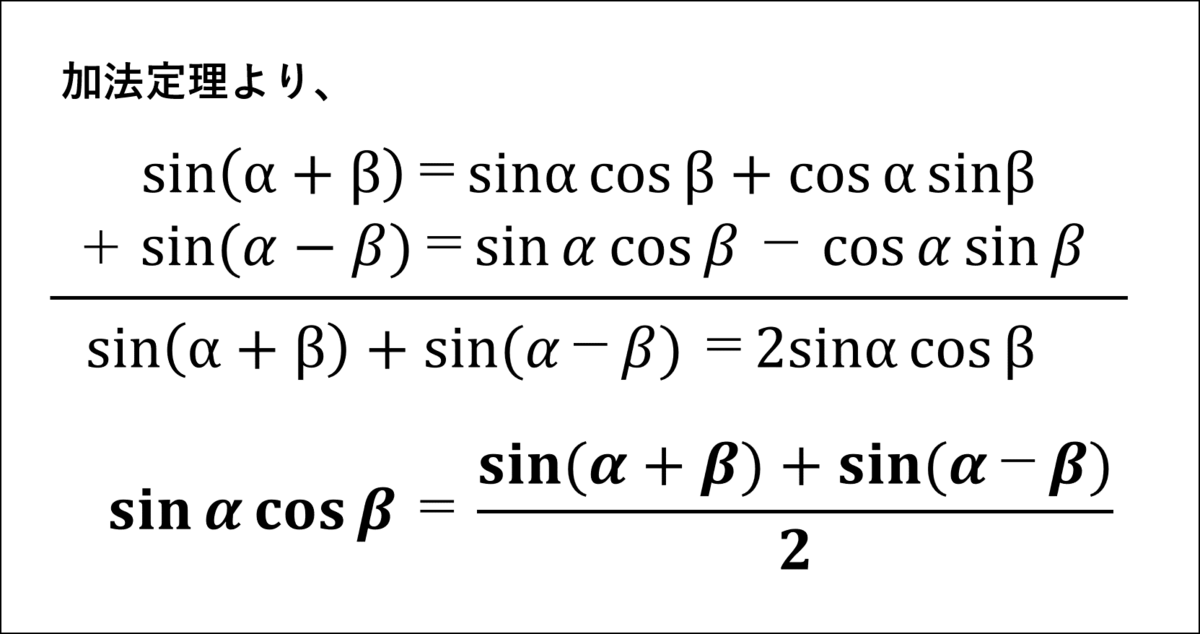
シエル:「次は『cosα・cosβ』だ。」
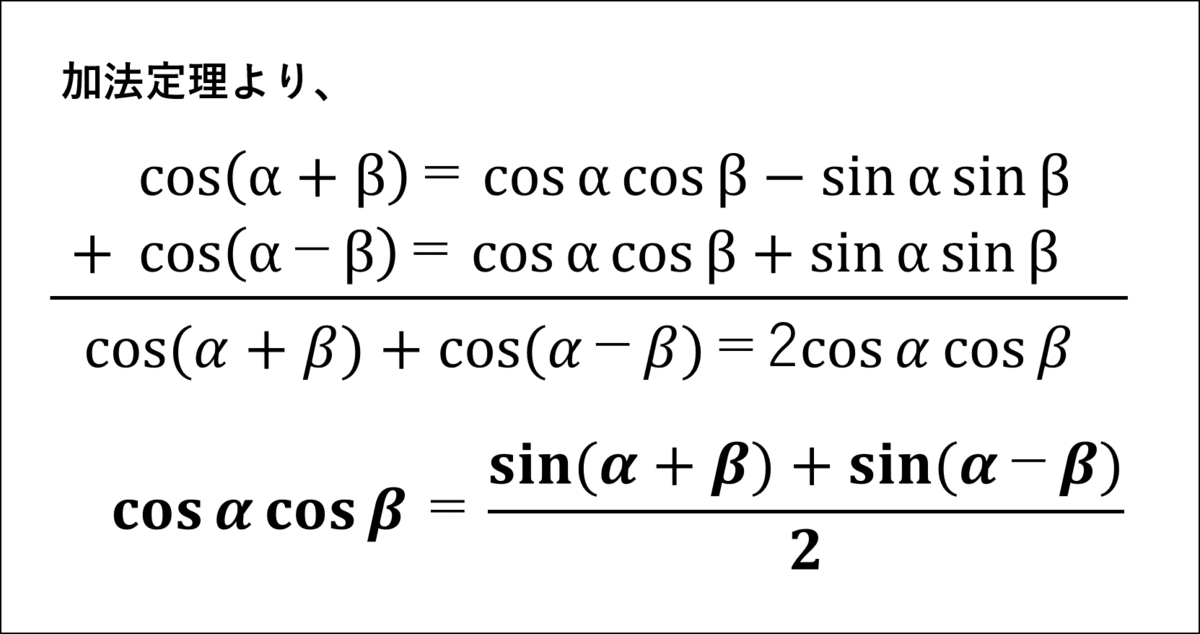
シエル:「最後は『sin²α』『cos²α』だ。
これには加法定理とは別に、もう一つの公式を使う…覚えているかな?
『sin²α+cos²α=1』」

シエル:「これで主要な三角関数の公式は概ね出揃ったよ。
まぁ…実際に使う時には、その都度振り返るから安心しろ!」
ミア「はぁ~疲れた…
私そろそろ限界かも。」
僕:「そうだね。
三角関数のフルコース…ミアもよく頑張ったと思うよ。」
シエル:「…まぁ、文系の2人としてはよく持った方だと思うよ。
じゃぁ、ここからの話は覚えなくてもいいから気楽に聞いてくれ。
三角関数の合成についてだ。」

三角関数の合成
シエル:「三角関数の合成は、正弦波と余弦派を組み合わせて、一つの正弦波の式に変換するテクニックだ。
![]()
ここで問題なのが、この公式の『a・b』がいったい何なのか?ということだ…
これを調べるために先ほどの加法定理を使う。」
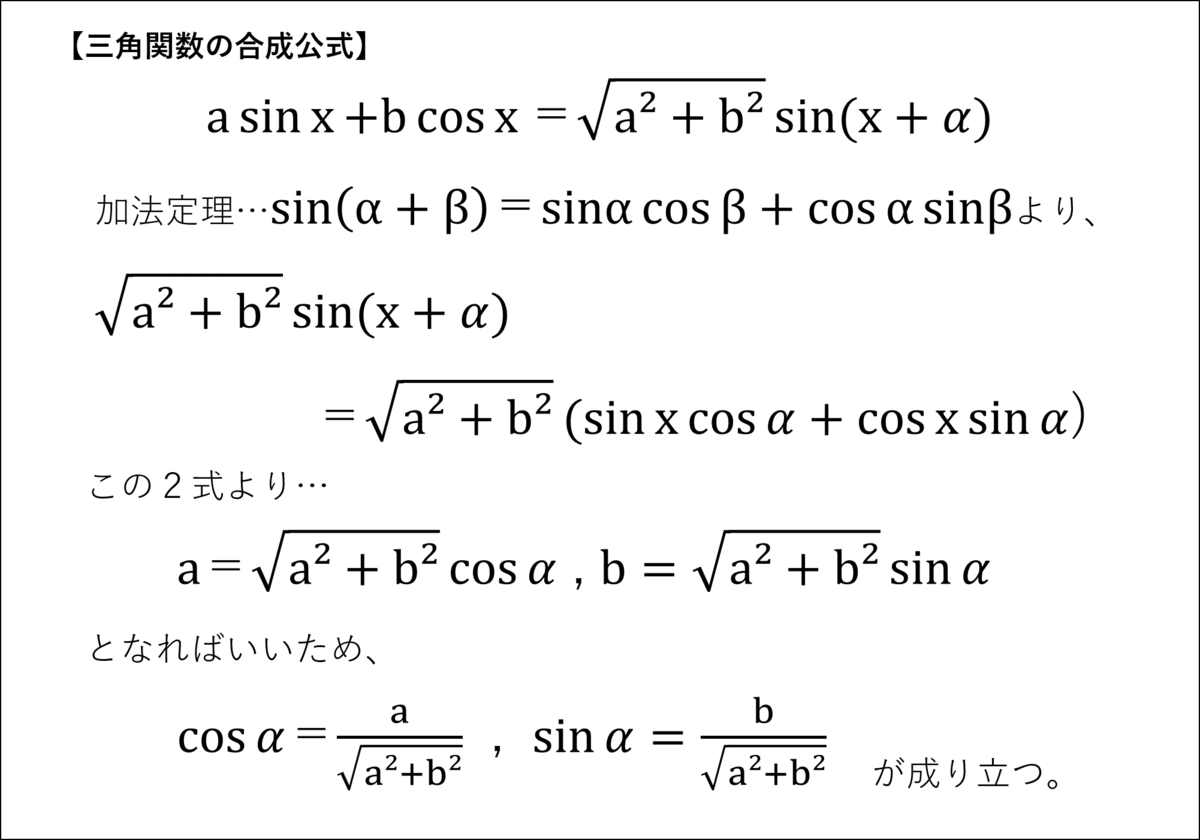
シエル:「これを踏まえて直角三角形を描けば、『a・b』がどの辺なのかわかるね。」
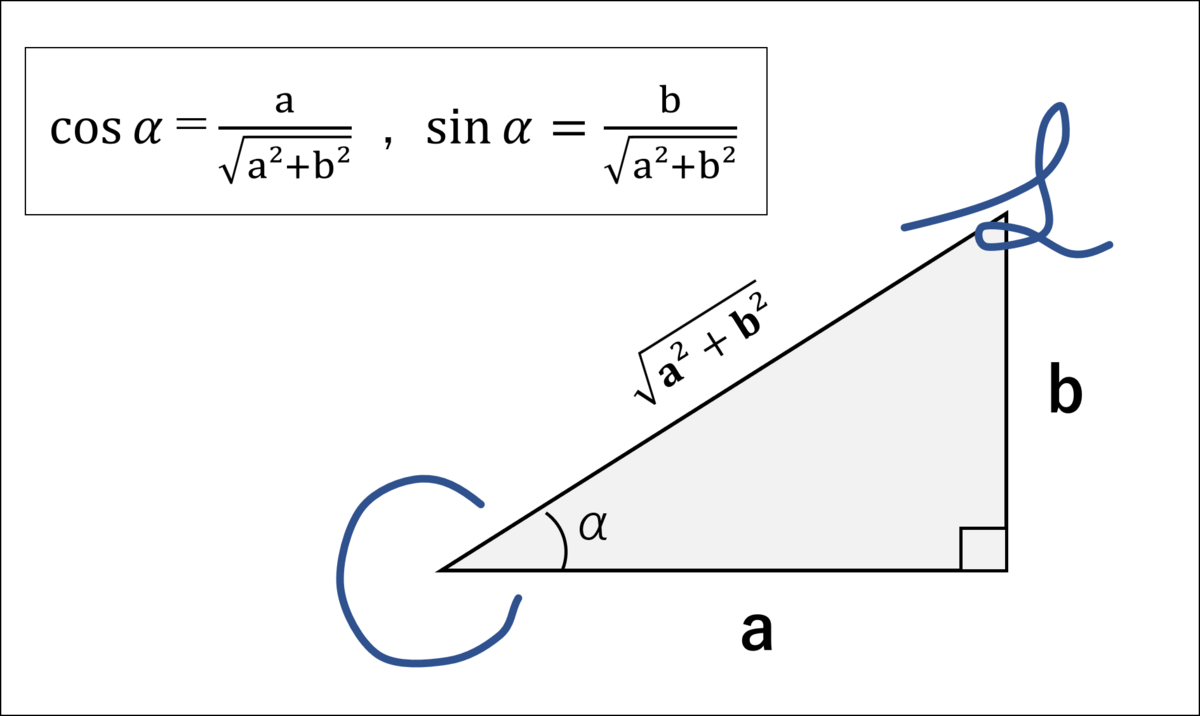
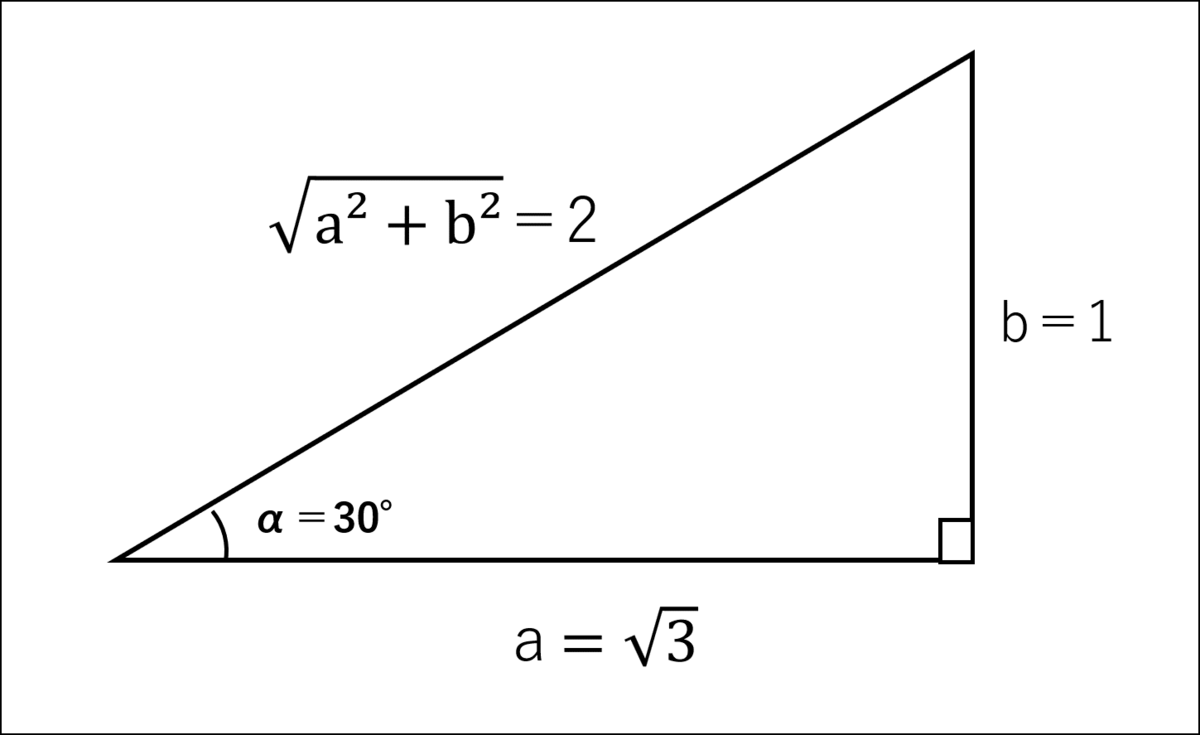
シエル:「例として、
『√3sinx+cosx』を合成させてみるね。
公式に当てはめると、
a=√3、b=1、斜辺が2だよ。」
シエル:「ここまでわかれば合成は簡単だ。
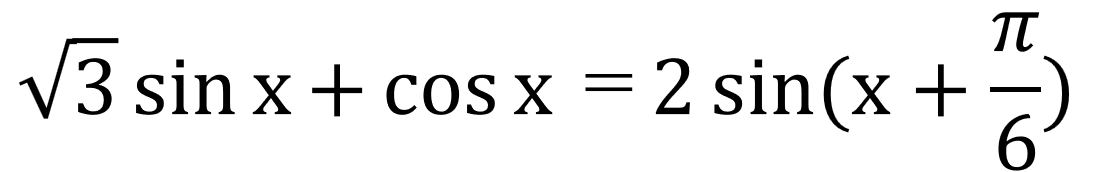
合成された正弦波を見てみよう。」
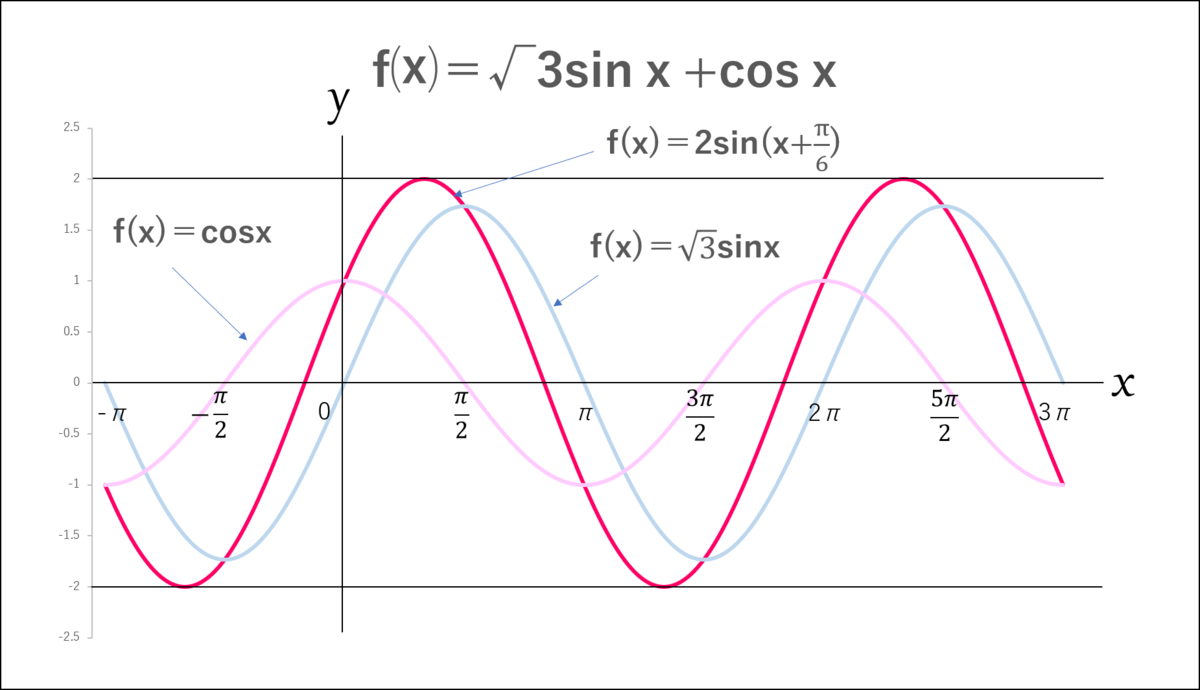
シエル:「このように、正弦波と余弦派を合成させると、
振り幅が|√a²+√b²|で、スタート位置(←これを位相と言う)がαだけずれた正弦波を作り出すことができる。
最後に、複数の正弦波を合成させて、複雑な波の形を作ってみるよ。」
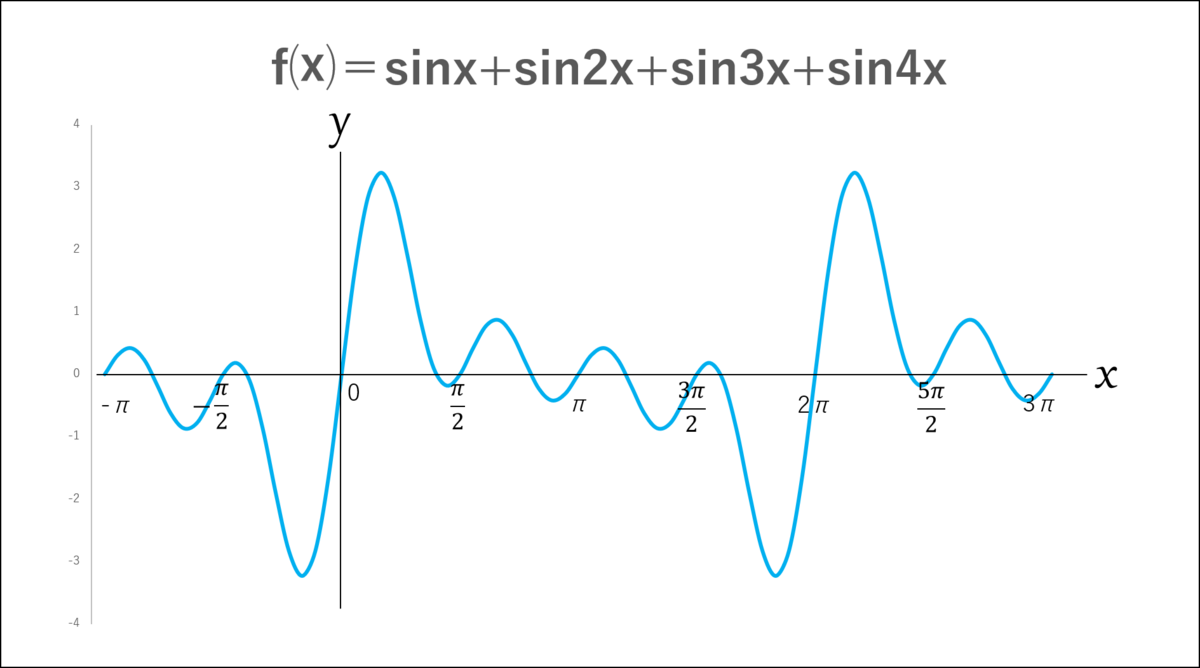
ミア:「なんだか正弦波ってクネクネしててかわいいね♡」
シエル:「おっ!ミアちゃん、いいこと言うね~♪
今日の授業はこれでおしまいだよ。」

この旅の終着点
僕:「ねぇシエルちゃん…そろそろ、『僕たちがどこを目指して進んでいるのか?』教えてくれないかな?
目的地が見えないまま、文系人が数学の勉強をやり続けるのは、正直キツイから…。」
シエルちゃんは少し間を開けてから口を開いた。
シエル:「・・・確かにそうだな。
波の解析について、私の目標は、ミクサがこの数式を理解することだ。」
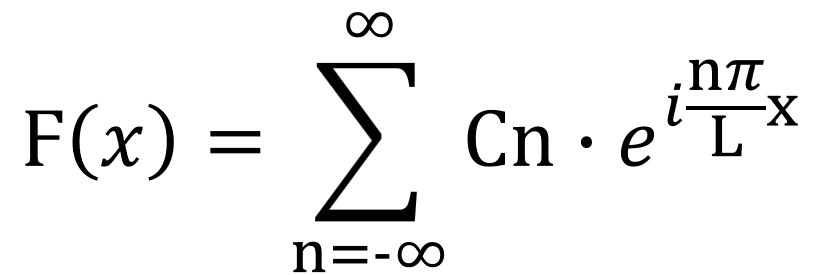
意外とシンプルな数式だな…でも、ほとんど意味がわからない。
まずは最初の総和記号の下にある『-∞』だ。∞にマイナスもプラスもないだろ!?
最後尾はオイラーの公式かな?
でも、分数の意味がわからない…。
そして最も謎なのが…
ミア:「シエル…真ん中にある『Cn』って見たことないけど、何なの?」
僕:「!?」
シエルちゃんは満足そうな笑みを浮かべて言う。
シエル:「2人とも、ちゃんと数式を読もうとしたね。感心感心♪
実は、この式は長くて複雑で美しくないから、『Cn』という記号で数式を折り畳んでいるんだよ。
『数列のa₁.a₂.a₃...an』みたいなものだよ。
じゃぁ、『Cn』を展開するよ。」
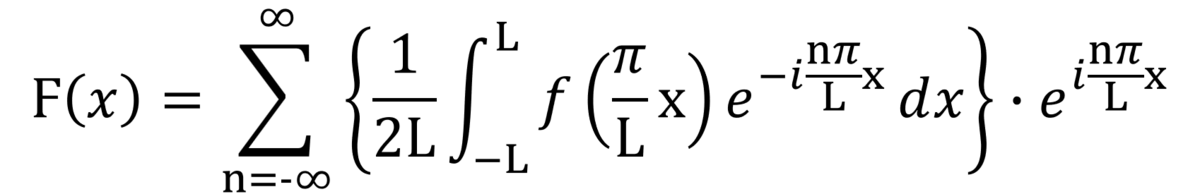
僕:「ハハハ、ガチなやつだ!」
シエル:「これは複素フーリエ級数と言って、波の解析における基本公式の一つだ。
数学者たちがこの式を追究し続けたからこそ、人類のテクノロジーはここまで進歩してきた。
投資家がこれを学ぶべき理由は2つある…
一つは、言うまでもなくチャート分析に応用可能だからだ。
多くの人とは違う視点で分析できれば、価格変動の隠されたシグナルを見つけ出せるかもしれない。
そして重要なのが二つ目の理由だ。
この式を理解するためには、三角関数を始め、シグマの計算、微分・積分、指数・対数、複素数の基礎知識が必要だが…
おそらく、全人類の50%以上が、これら知識を理解しないまま一生を終える。
つまり、この式が理解できれば、50%以上の人間を数学知識で出し抜けるということだ!」
僕:「"投資の利益は、自分以上の愚か者を何人増やせるかによって決まる"…か。
確かに、闇雲に数学を勉強するよりも、これを理解した方が早そうだね。」
ミア:「あの…私も、このまま付き合おうかな…
もう、頭のいい人に利用されるのはイヤだから。」
シエル:「決まりだね。
では、今後の目標を『複素フーリエ級数を理解する』ことに定める!
そして次は、文系殺し四天王が一人、微積分を攻略する!」
ミア:「高校時代の恨みを晴らさせてもらわないとね!」
僕:「ミア…僕たちは文系で、そもそも高校時代に微積分を習ってないから、恨みは無いはずだよ。」
ミア:「え…そうなの!?」
人生、山あり谷ありだ。
良い事があれば、悪い事もある…
会社の経営が"本格的に"傾き始めたのは3年前からだ。
正直、この先どうなるかなんてわからないけど、『倒産』の二文字が脳裏をよぎる。
『終身雇用』が都市伝説だったことを知り、
『一流企業の従業員』という僕のアイデンティティは完全に砕かれた。(恥ずかしながら本当にそう思ってた…)
このことはまだ、ミアには言えてない…。
僕に残された時間は、あとどのくらいだろうか?
早く、計画を進めなくては…脱社畜計画を。

参考書籍
文系編集者がわかるまで書き直した 沁みる「フーリエ級数・フーリエ変換」
東大の先生! 文系の私に超わかりやすく高校の数学を教えてください!
東大の先生! 文系の私に超わかりやすく数学を教えてください!