CONTENTS

人生、山あり谷ありだ。
良い事があれば、悪い事もある。
でも、悪い事が続いたからといって、次良い事が起きてくれるわけではない。
人生が描く波形は、とても複雑で、それでいて不規則だ。
この残酷なシステム下で、
すべての人に共通する唯一の救いは、この波には"終着点"があること。
問題は…技術の進歩が終着点を遠ざける一方で、ショートカットするのも決して容易ではないことだ。

文系投資家の修行~三角関数は投資家を救うのか?~【前編】

再会
シエル:「喜べミクサ!今日もシエルちゃんとおしゃべりする権利が与えられたぞ!」
僕:「え~っと…今日来る予定だったっけ?」
ミア:「あ!そういえばそんなこと言ってたような…。」
シエル:「おい!まさか、このくだり毎回やるのか!?」
ミアは僕のパートナーで、シエルちゃんはミアの妹だ。

数学は大の苦手分野だけど、投資家としてそうは言っていられない…
数学の本を数ページ読んでは項垂れる…そんなことを繰り返していた僕を、たまたま家に来た数学オタクのシエルちゃんに目撃され、それを機に僕は彼女に波の解析法について学ぶことになった。(参照)
今日は、のんびり過ごしたかったんだけど...。
シエル:「ゲホッ、ゲホッ!」
・・・咳?
ミア:「ちょっと…もしかして風邪ひいてる?」
半ばキレ気味のミアの問いかけに対し、シエルちゃんは平然と答える。
シエル:「大丈夫だ!少し風邪気味だが…問題はない!
気は遣わなくてもいいぞ。」

『逆に、少しは気を遣ってくれ…。』
そう思ってしまった僕は無慈悲な人間なのだろうか。
ミアは呆れた顔で言う。
ミア:「はぁ~…今日一日家で寝て、風邪を治すという選択肢は無かったわけ?」
シエル:「ゲホッ、ゲホッ!ズズーーー!(鼻をかむ音)
そんな選択肢はない!
だって誰もいない家に一人で寝てるなんて寂しいじゃん!」
僕:「その気持ちは少しわかるな。」
ミア:「なに共感してるのよ…もう風邪ひいて来るのはこれっきりにしてよ。」
シエルちゃんはニカッと笑いながら言う。
シエル:「二人とも理解が良くて助かるよ。
オジャマしま~す。」

サイン・コサイン…
僕たちはリビングのテーブルへと向かう。
シエル:「今日は冷えるねぇ、外は一段と寒かったよ~。
ミクサ、何かあったかい飲み物はないのか?」
僕:「はいはい先生わかりましたよ~。」
そう言って僕は生姜湯を作ってシエルちゃんに手渡す。
シエル:「おー!生姜湯とは気が利くね。
少し甘さが足りないが…風邪ひいてるときに飲むと、なんとも美味だねゲホッ!」
僕:「まったく…風邪ひいてるのに、よく数学の話なんてしようと思えるよね…
今日は、なにを教えてくれるのかな?」
シエル:「今日は波の解析の基本、三角関数についてだ!」
ミア:「波を解析するのに、三角形?」
シエル:「三角形バカにすんなよー!すごいんだぞ三角形は!
ミクサは『三角比がどういうものか?』くらい知ってるよね?」
いきなりか!えーと…
僕:「サイン・コサイン・タンジェントだね。
直角三角形の左側の角度がわかれば、2つの辺の比率がわかる…で合ってるかな?
確か…直角三角形の3辺には、斜辺・対辺・隣辺という名前が付いていて、高校生の頃はサイン・コサイン・タンジェントの頭文字を筆記体で書いて、どの辺の比か覚えたよね。」

シエル:「よし、じゃぁ次に、θ=30°の代表的な直角三角形について考えよう。
θ=30°の直角三角形は、対辺:斜辺:隣辺=1:2:√3と決まっているから…
それぞれの辺の長さを1㎝・2㎝・√3㎝としよう。
ミアちゃん、sin30°はいくつになる?」
ミア:「へっ?私もやるの!?
う~ん…sinは斜辺分の対辺だから…」

ミア:「わかった!sin30°は2分の1!」
なんだかミアは嬉しそうだ。
シエル:「正解ゲホッ!
数学が嫌いな人は、大体ここで『わからない』と即答するからね…。
で…ゲホッ教えようとしても『使わないから』と言う…。
ミアちゃんはスゴイよ!だって考えたんだもん!」
ミア:「これくらい楽勝だし!」
シエル:「じゃぁ、斜辺の長さが10㎝になりました。
この三角形の高さは何センチゲホッ?」

ミア:「えーっと…わからない。」
僕:「さっきsin30°がいくらになるかわかったから、それを使うんだよ。」
ミア:「わからない!そもそも私『波の解析』とか興味ないし!
三角関数とか…使わなくても生きていける自信あるし!」
僕・シエル:「あ~…。」
シエル:「sin30°が2分の1とわかってるから、これを使えば簡単に解けるよ。」

シエル:「この三角形の高さは5㎝だよ。
ちなみに、cos30°についても同じように出せる。」

シエル:「タンジェントについては波の解析では使わないから、割愛するよ。
これで三角比がどういうものかわかったね。ゲホッ
じゃぁ、本題に入ろうか!」

三角形から円へ。
シエル:「じゃぁ、本題に入ろうか!
三角関数はθの値が変化することでsinθ・cosθの値がどう推移するかを表したものだよ。
これを知るために、舞台を三角形から半径1の円『単位円』に移す!
座標平面上に単位円を描いて、その円周上を移動する点pについて考えるよ。」

ミア:「出たよ『動く点p』!動かないでじっとしとけ!」
シエル:「・・・ゲホッ、いいかな?
この点pと原点を線で結んで、x軸とのなす角をθとする。
そして、点pからx軸に垂線を引っ張れば…」

シエル:「このように直角三角形が現われるゲホ!」
ミアは小声でつぶやく。
ミア:「なんだか線が微妙にずれてるから、直角三角形に見えないね。」
僕:「ゲホゲホ言いながら線を引いていれば誰だってこうなるよ。
直角三角形に見えている提で話を聞いてあげよう。」
シエル:「聞こえてるぞ。悪かったな!
…ミアちゃん、θの値が30°だったら、
点pのx座標とy座標はそれぞれいくらになる?」
ミア:「え~と…さっきやった計算だね。
半径が1だから、斜辺は1㎝で、
点pのy座標は対辺だからy㎝、
x座標は隣辺でx㎝として…
θ=30°だから…こういうことだよね?」

ミア:「sin30°とcos30°の値はわかっているから…」

ミア:「できた!
え…でもこれって…?」
流石、ミアは呑み込みが早いな…。
シエル:「そう!
点pの座標は(x=cosθ,y=sinθ)なんだ!
あとピタゴラスの定理から
『sin²θ+cos²θ=1』が成り立つ。
これは重要な公式だから覚えておいてね。」

シエル:「ゴホッ…次はミクサ!
θの値が60°のとき、点pの座標はどうなる?」
僕:「これは簡単に出せるね。
さっきの三角形をひっくり返して回転させたらいいだけ。」

僕:「θ=60°の点pの座標…つまり、
x=cos60°=1/2
y=sin60°=√3/2…だね。」
シエル:「まぁ、簡単過ぎたね。ゲホッ
ついでに、θ=45°の場合も考えておこうか。
θ=45°というと、直角二等辺三角形だね。
直角二等辺三角形の辺の比率は
『1:1:√2』と小学校?いや中学校か?
ゴホッ…どっちでもいいわ!で習ったね。」

シエル:「θの値が決まれば、sinθ・cosθの値が一つだけ確定する。
これが三角関数だよ。
今調べたものをまとめておくよ。」


正弦波
ミア:「ちょっとシエルいい?
θの値が90°まではわかったけど…もっと大きな…
たとえばθ=300°とかだったらどうなるの?」
シエル:「θの値が0~180°の間は反時計回りに点pを動かせたね。
ズズーーー(鼻をかむ音)
180°以上の場合は、逆に時計回りに点pを動かせるとわかりやすいよ。
たとえば、θ=300°は、θ=-60°と同じだね。」

シエル:「座標平面は4分割されていて、それぞれを第一~四象限と呼ぶんだけど…ゲホッ!
sinθ・cosθの符号は、点pの位置によって変化するから、慣れないうちは図を描いて確認するようにしておくと間違いを減らせられるよ。」

ミアは小声でボソッとつぶやく。
ミア:「まぁ…使わないけど。」
シエル:「よし。これで三角関数の基礎を復習することができた。
『三角形』から『円』…そしてようやく、ここから舞台は『波』へと進む!
θの値が0~360°まで変化した際のsinθの値の推移をまとめると、こうなる。」

シエル:「そして、ゲホッこれをグラフ化してみると…」
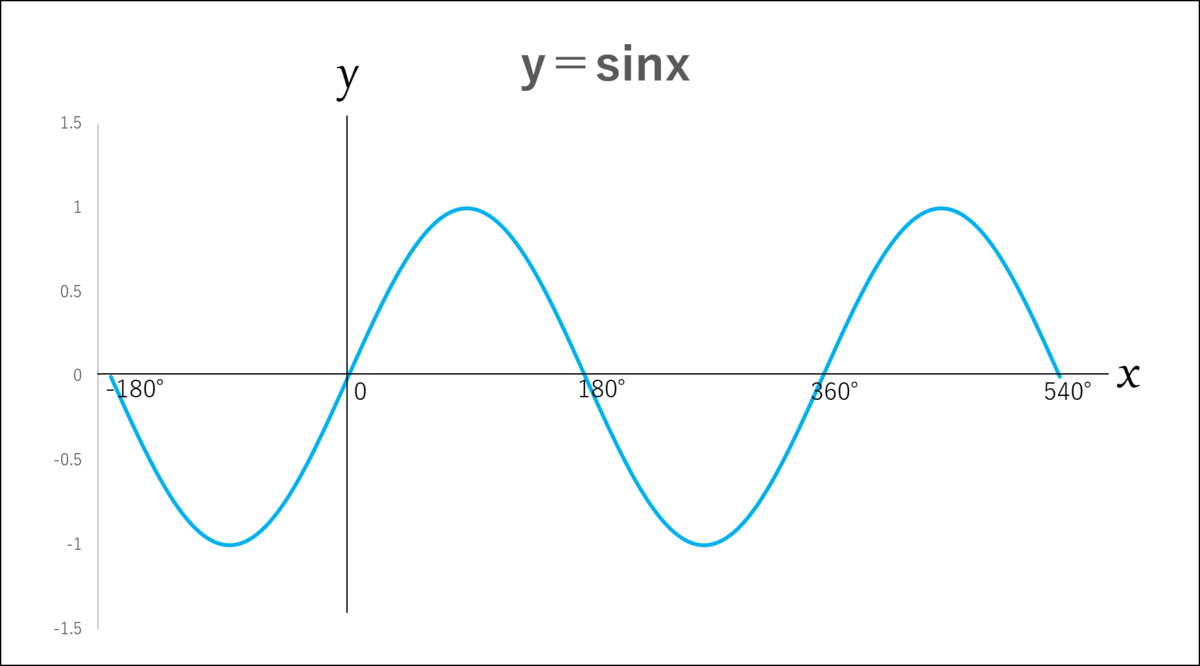
ミア:「波だ!」
僕:「不思議だな…高校生の頃に習ったはずなのに…初めて知る感覚だ。」
シエル:「これが正弦波だ!
あとで説明するけど、cosθの推移が生み出す『余弦派』も、正弦波の一部だ。
これから正弦波について詳しく見ていきたいところだが…
残念なことに私はまだ、お昼ごはんを食べてない。」
ミアは軽蔑の眼差しをシエルちゃんへ向ける。
ミア:「シエル…まさか食費浮かせるためにここに来たんでじゃないわよね!?」
シエル:「まさか…ゴホッ!
私が、そんなことするセコイ人間だとでも!?
だが、あいにく今は金欠ゆえにカネがない。
ミクサ、どうする?
ゲホゲホッ…病気の妹を、空腹のまま帰らせるのは…さぞや後味が悪いことだろうな!
それに、三角関数のおもしろいのはここからだぞ!」
僕:「確かに、かなり後味が悪そうだな…。
・・・デリバリーでいいかな?」
シエル:「ゴチになる!」
ミア:「今月は生活費カツカツだから、代金はミクサが払ってね!」
このタイミングで生活費がカツカツ!?
電気代が原因か?電気代が上がったからなのか!?
うっ…昼食3人分…小遣い制の社畜は救われないな…。
後編に続く。
