※当記事は前回からの続きです。
CONTENTS
『たくさん失敗することはいいことだ。だって、それだけ挑戦したということなんだから。』
あのころの僕は、そう信じていた。
いや、そう信じたかった…。
でも…そうじゃなかった。
この世界には、失敗する者の居場所なんて用意されていない。
傷付かずに生きていくには、成功し続けなければいけない。
だから、僕は欲した。
失敗を避けられるだけの知識を。
未来を予測する方法を。

資産運用から生まれた不思議な数字は投資家を救うのか!?

投資で勝つ"手段"としての数学
???:「起きろー!」
僕:「…ん~?」
寝てたのか…なんだか騒がしいな…
???:「起きろー!そして喜べ!
シエルちゃんが泊まりに来てやったぞ!」
・・・シエルちゃんはミアの妹で、三姉妹の次女だ。

おそらく、30人に1人くらいの確率で生まれてくる天才…だと思う。(数字は微妙だけど…)
天才の定義は曖昧だけど、たぶん「勉強が楽しい」とか言う狂人のことを指すのだろう。
僕:「えーっと…今日来る予定だったっけ?」
ミア:「この前言ったじゃん!また話聞いてなかったんだね!?」
ミアは僕のパートナーだ。

彼女には、僕が集中して何かに取り組んでいるときに、狙ったかのように重要なことを告げる妙な癖がある…。
シエル:「本を読みながら眠りにつくのは至福のひとときだね!わかるよ~。
なんの本を読んでたのかな~?えーっと、
『超簡単!サルでもわかる数学のキホン』
・・・あ~…。」
相手から「あ~…」という反応が返ってくるのは、地味に傷付くものである。
この短い言葉には"哀れみ"や"軽蔑"といった負の感情が詰まっているからだ。
僕:「数学が得意な人は、そうでない人よりも予測の的中率が高いって、本で読んでね…それで数学の本を読むことにしたんだけど、いつも読み始めてほんの数分で睡魔に襲われるんだ。」
シエル:「ふーん。たぶん眠くなるのは、ミクサが数学を勉強すること自体を目的にしているからだよ。
数学は"目的"じゃなくて"手段"だよ!
ミクサは投資で勝つ方法を知りたいんだよね?
・・・そうだな~、
私が特別に"投資で勝つための手段としての数学"を教えてあげよう!」
僕:「あー…でも、数学の本は何冊も読んできたけど、投資で使えそうなものは無かったよ。」
シエル:「へ~。
『マンガでわかる』『文系でもわかる』『サルでもわかる』…
この程度の本しか読んでないのに、"使えない"って決めつけるんだね。
・・・クロード・シャノン。」
僕:「うっ…」
ミア:「クロード・シャノンって、だれ?」
僕:「天才数学者であり世界一の投資家だよ。
クロード・シャノンは約25年間で年平均28%という驚異的な利益率を叩き出したそうだ。
ちなみにこの記録は、彼の死後20年を経た現在でも破られていない。」
シエル:「世界一の投資家が数学者なんだから、数学が投資で使えないわけがないでしょ!
まぁ、とりあえず聞け!そして驚嘆しろ!
この私、天才シエルちゃんが、文系のミクサでも理解できるように、
『波』を解析する方法を教えてやろう!」

虚数(i)♡
シエル:「天才シエルちゃんが、文系のミクサでも理解できるように、
『波』を解析する方法を教えてやろう!」
僕・ミア:「波の解析?」
シエル:「世界のあらゆるものは波で動いている。
光・音・人間の感情もそうだし、株式の値動きだって波でできている。
もし、波の動きを知ることができたら…それってすごいことだと思わない!?」
僕:「そんな大それたことが文系の僕にできるとでも?」
シエル:「それはミクサ次第だよ。
まぁ、理解できなくても数学の基本は身に付く。
きっと、これを知れば世界の見方が大きく変わるはずだよ!」
僕:「そっか…じゃぁ、ダメ元で聞こうかな。」
シエル:「いいねぇ~ダメ元!
ミクサがどこまで知っているのかわからないから…
とりあえず、この方程式解いてみて。」
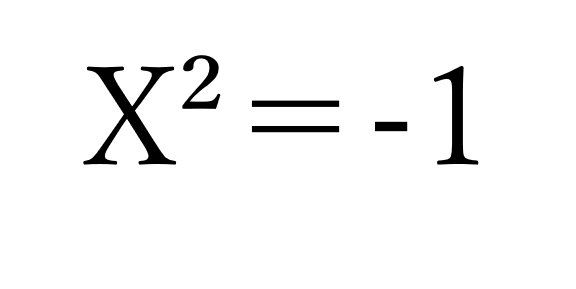
ミア:「ちょっとシエル!それはさすがに舐めすぎだよ!」
シエル:「そっかな~、たぶんミアちゃん間違えてると思うよ。」
僕:「中学生の問題だね。」
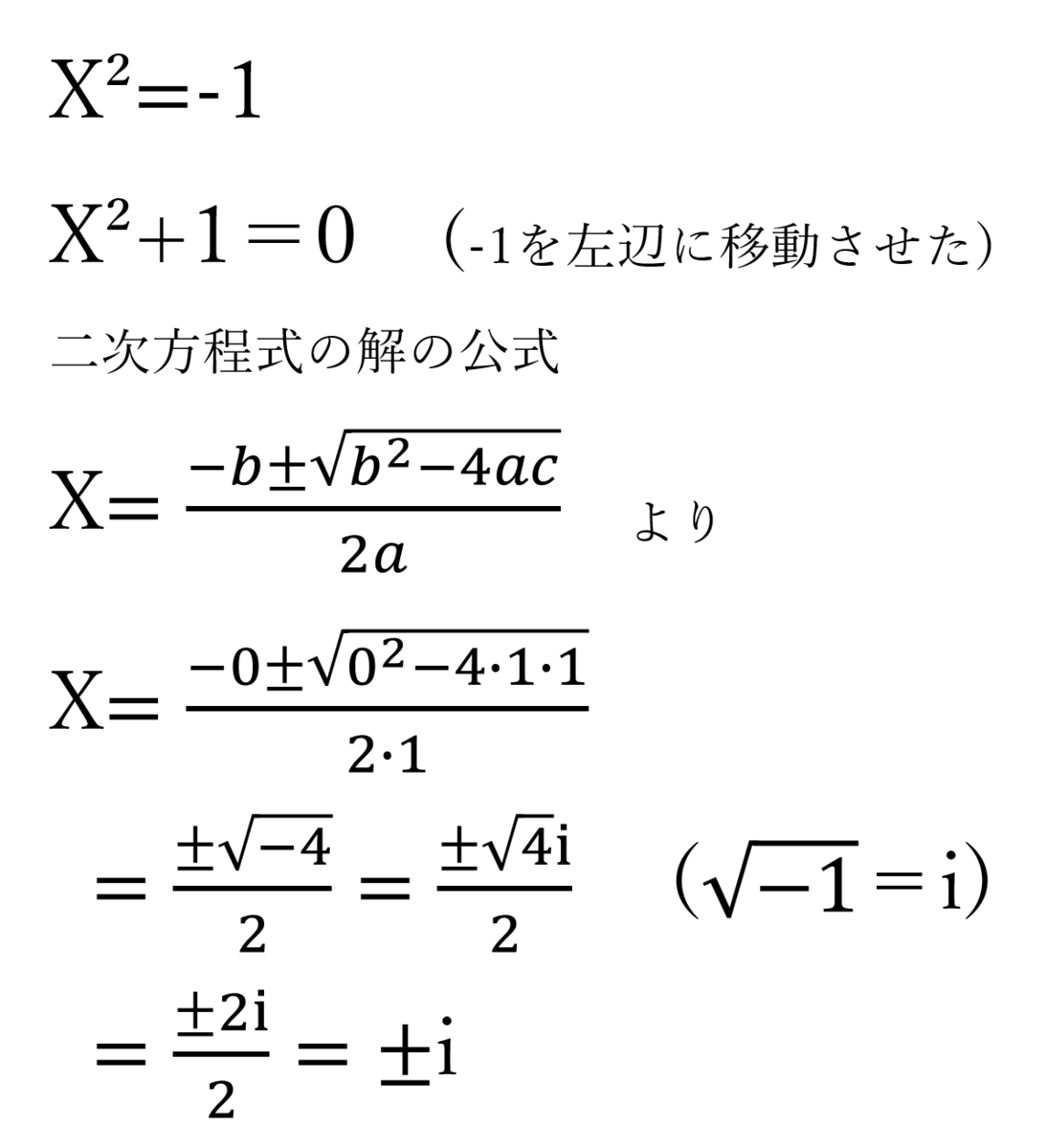
僕:「答えは『X=±i』だね。」
ミア:「なに…途中の変な式…」
僕:「『二次方程式の解の公式』だよ。
まぁ…普段使わないし、忘れてるのは無理ないよ。
2乗して-1になる数は、虚数単位iっておいてたよね!
懐かしいね。」
ミア:「・・・」
シエル:「ちっ…騙されなかったか。
じゃぁ、この数字は何かわかる?」
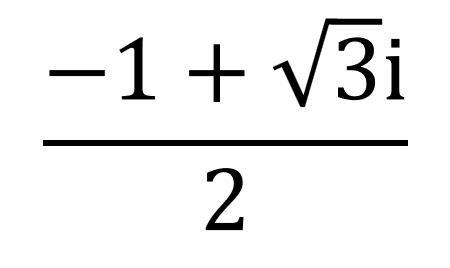
僕:「オメガ(ω)だね。」
シエル:「ほー、これを見てすぐに『ω』を連想するか!」
ミア:「勝手に2人で盛り上がらないで!
なによ?その『ω』って。」
僕:「『1』にこの数字を3回かけると『1』に戻るんだよ。」
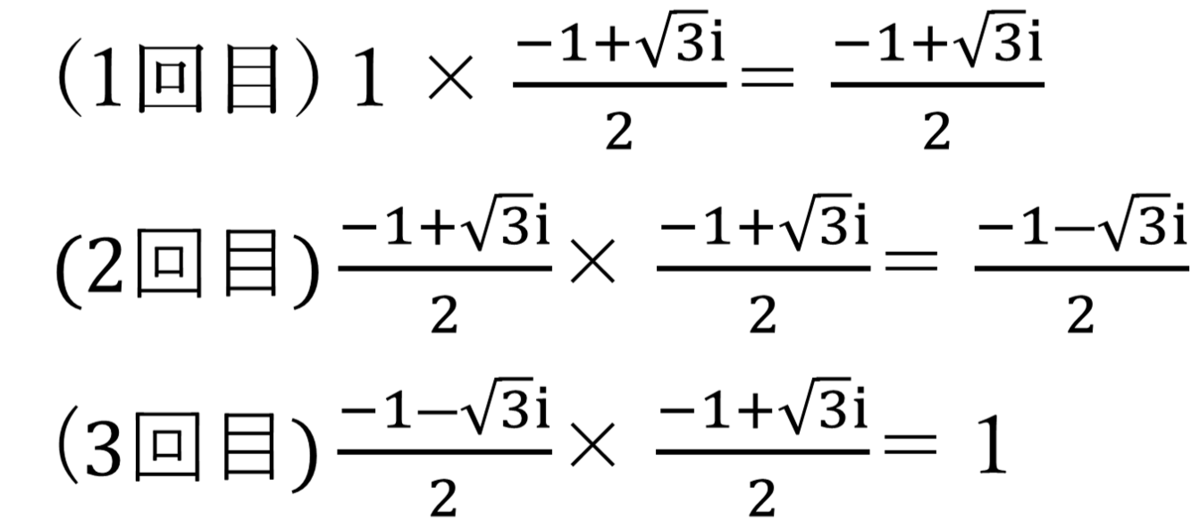
シエル:「で、この数字をωと置くと、『3回かけると1になる』性質から、こんな感じで計算できる。」
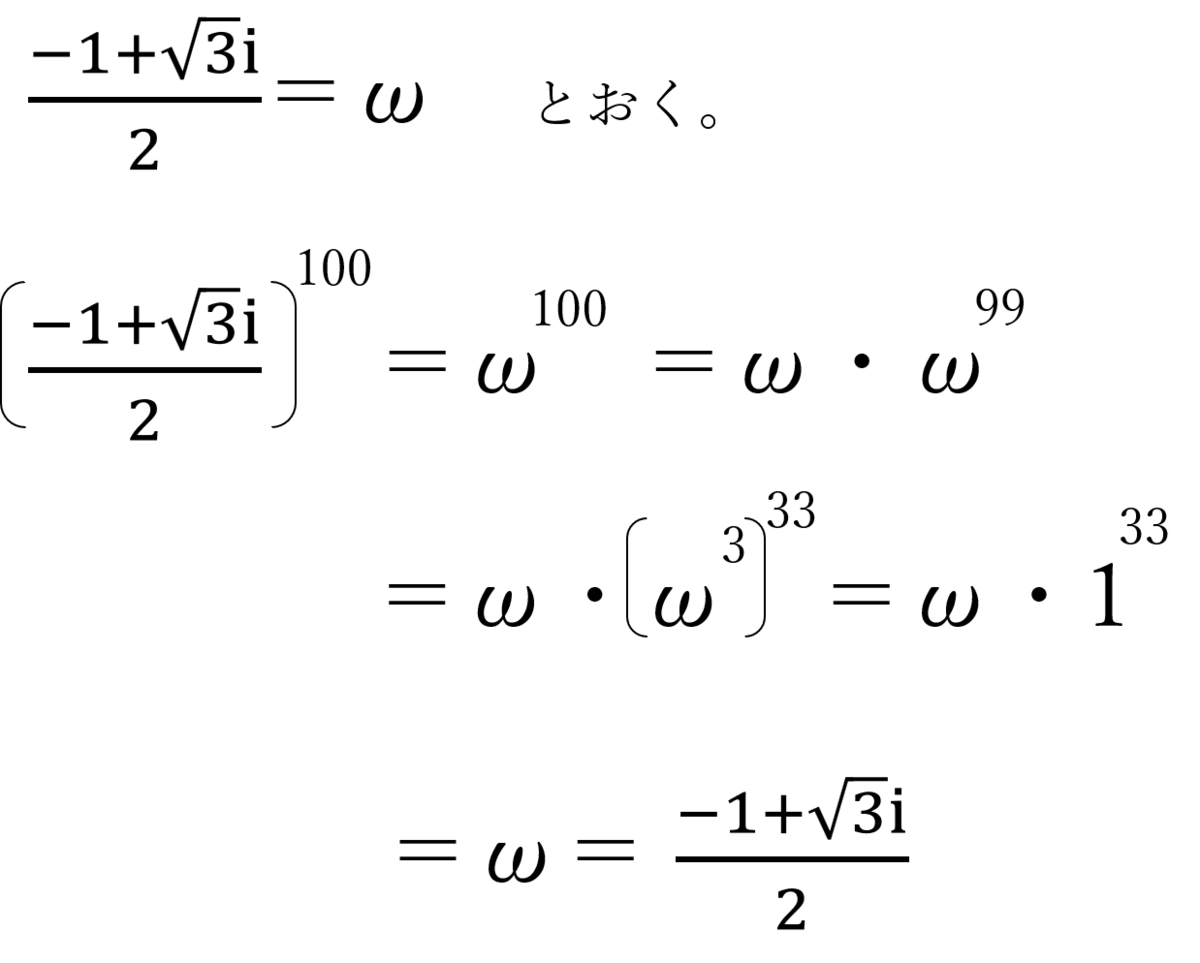
僕:「でも、これは遊びだね。知ってたところで、何の役にも立たない。」
シエル:「そうでもないさ!
これは虚数の掛け算における重要な性質を表しているんだよ。」

見えなくても存在する。
シエル:「これは虚数の掛け算における重要な性質を表しているんだよ。
私たちが普段使っている数字…つまり実数はすべて、数直線上で表すことができるよね?」
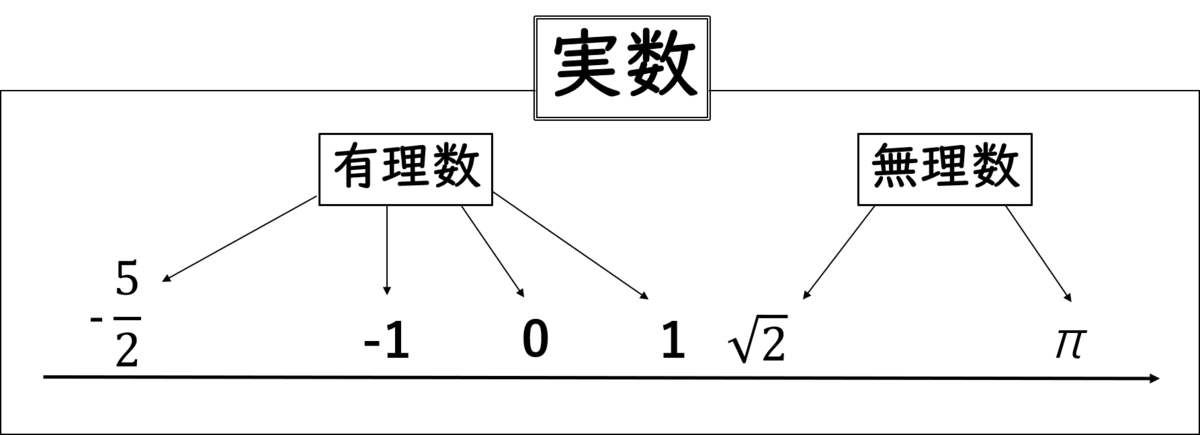
ミア:「うん。じゃぁ、虚数はどうやって表すの?」
シエル:「虚数は『数直線上の外』に存在してるから、縦にもう一本線を引っ張って…」
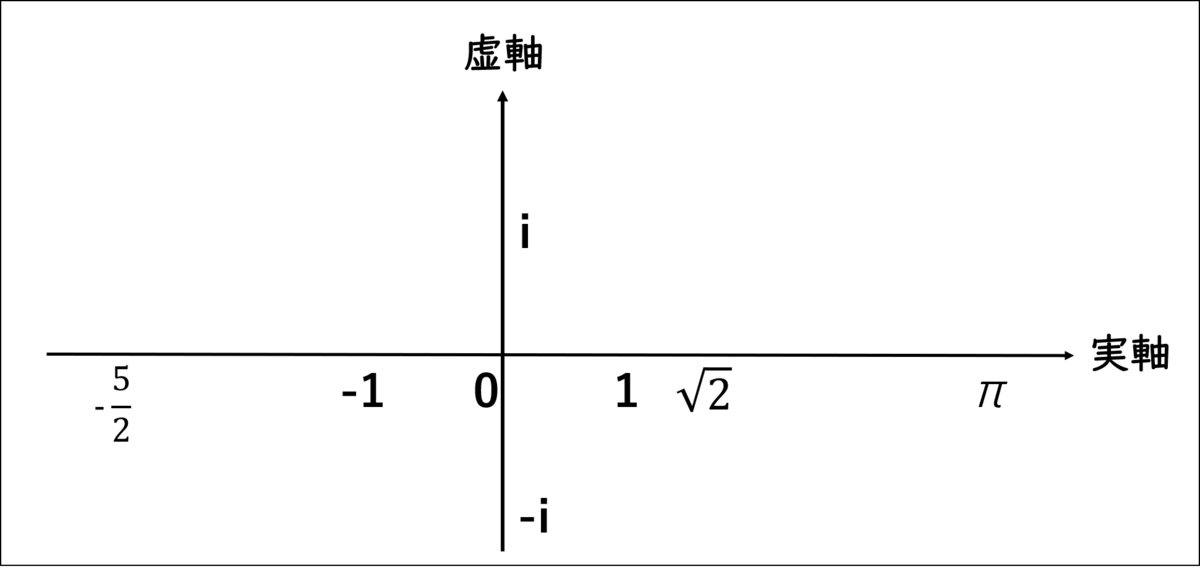
シエル:「こうすれば、虚数が存在していることがわかるよね。
実数の数直線は実軸、縦に引っ張った線は虚軸と言って、
虚数の位置はこの平面を使って捉えるんだ♪
この平面全体のことを複素平面という!
そして、複素平面上にある数字はすべて複素数と呼ばれているよ。」
ミア:「専門用語ばっかり…一気に勉強感でてきたわ…もどして!」
シエル:「そうだね。お堅い話はこれくらいにしようか。
じゃぁ、ωを複素平面上に表してみるね。」
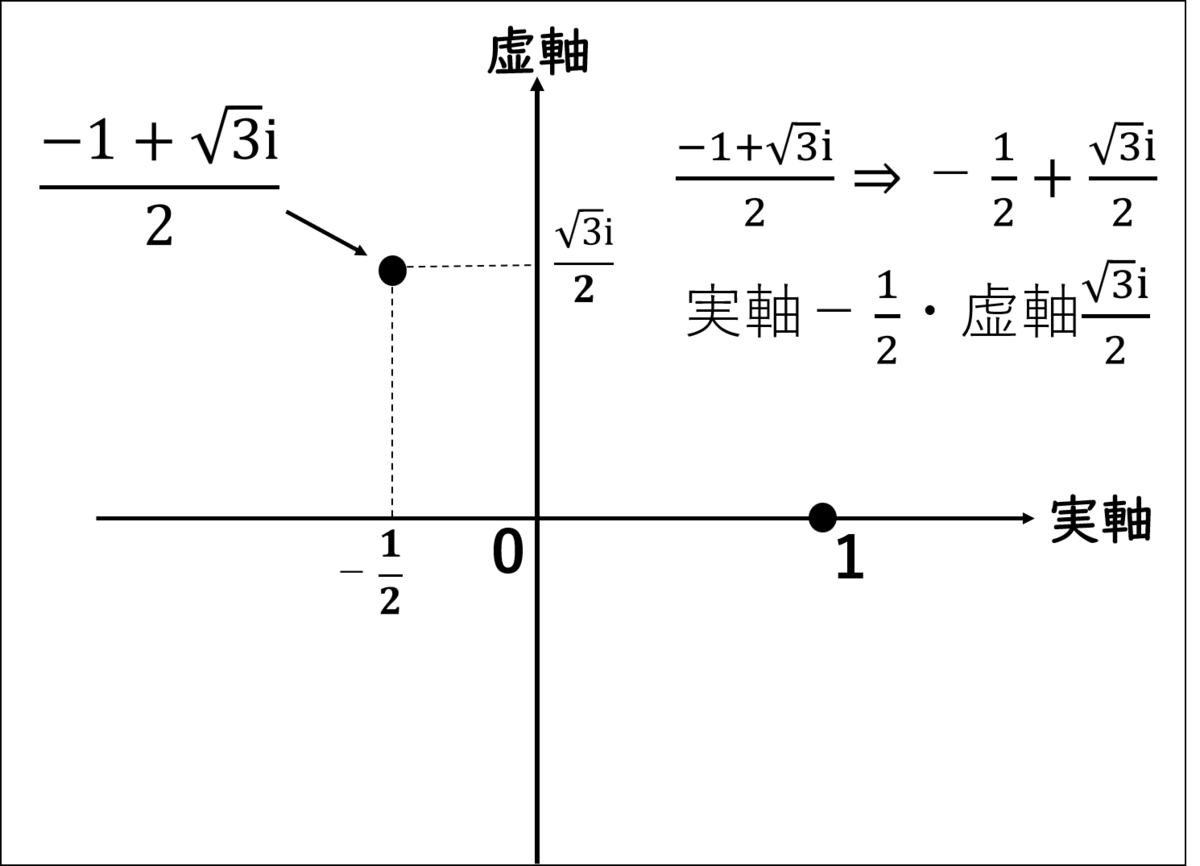
ミア:「もう一つは私が書き込むね!」
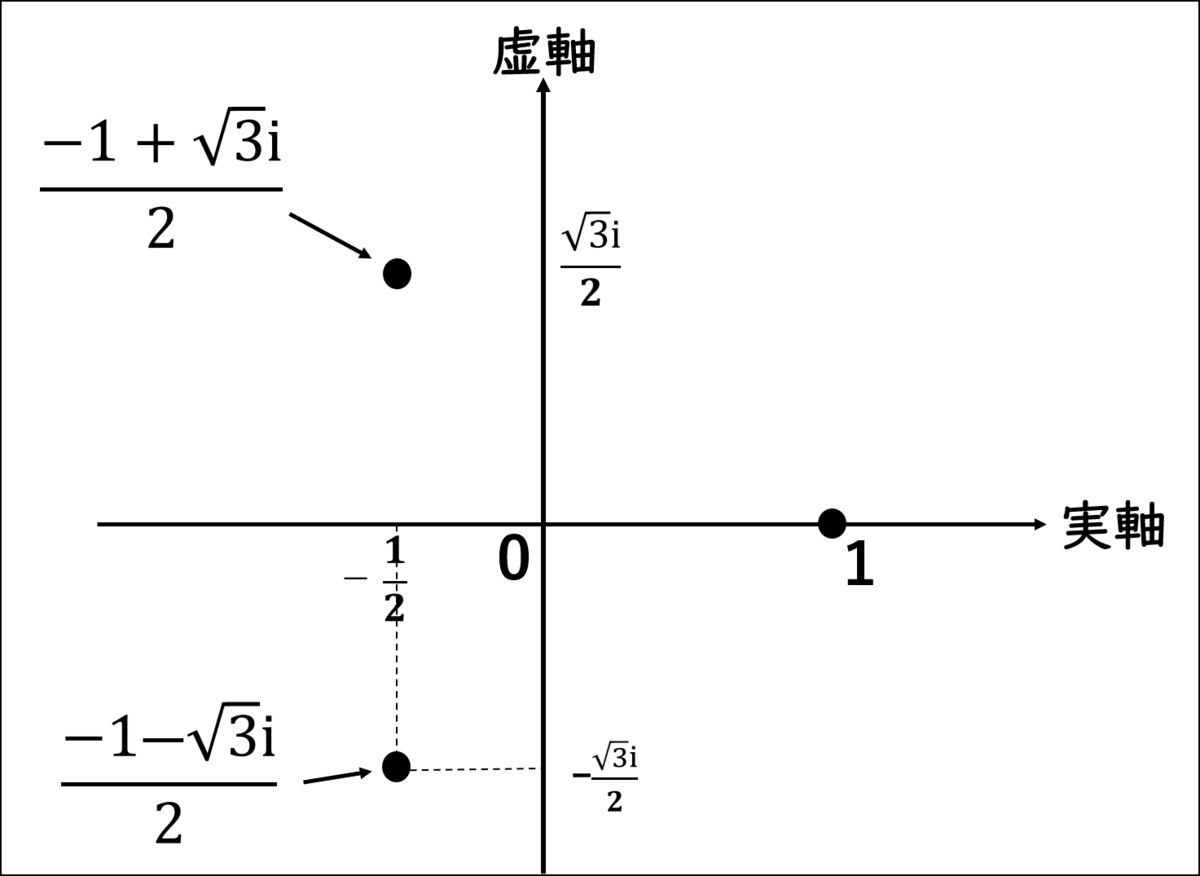
僕:「回転してるのか!?」
ミア:「なにが?」
シエル:「その通り。複素数に虚数をかけると、座標が回転するんだよ。」
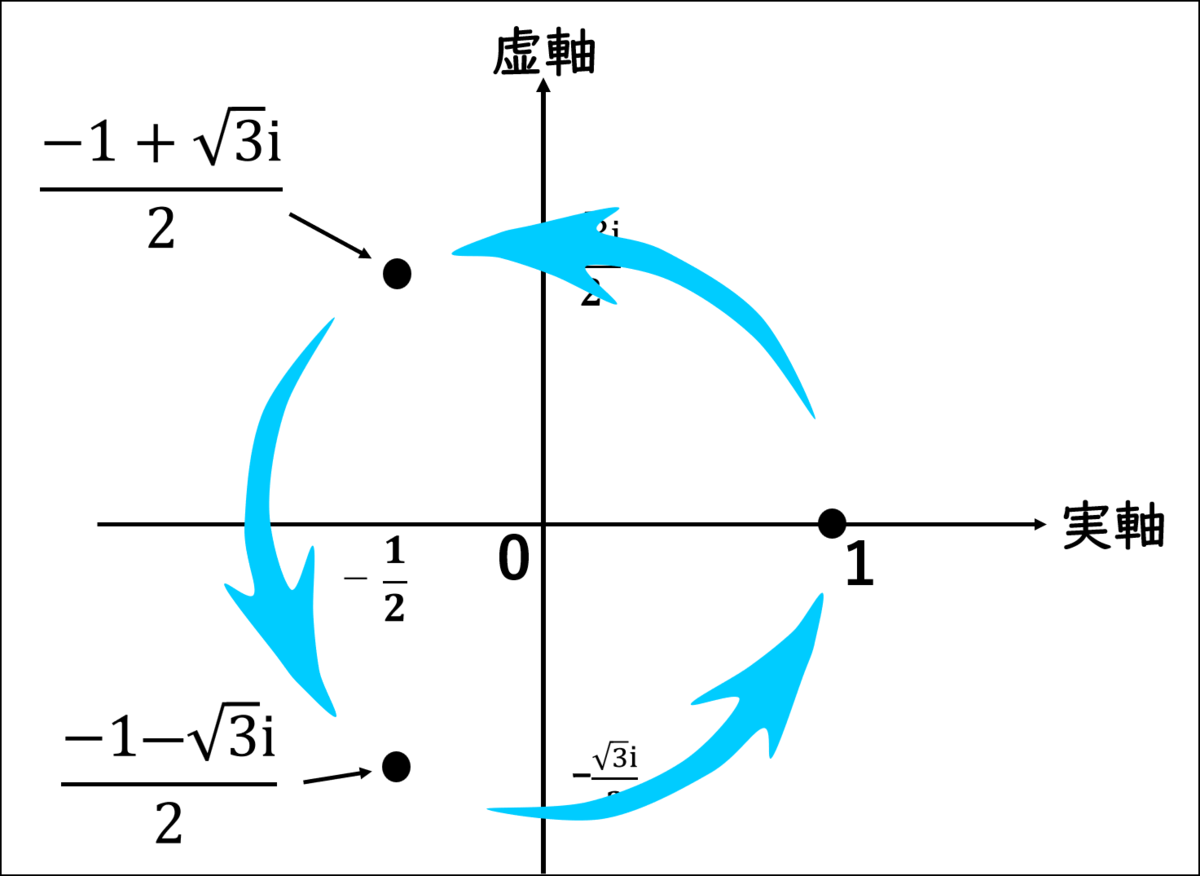
シエル:「もう一段話を進めるよ!
ミクサは投資の勉強をしてるなら、"資産運用から生まれた数字"は知っているよね?」

資産運用から生まれた数字
シエル:「投資の勉強をしてるなら、"資産運用から生まれた数字"は知っているよね?」
僕:「ネイピア数のことかい?」
ミア:「ネイピア数ってあの2.71828…ってやつ?」
僕:「うん。たとえば、
年利100%で元本保証付きの金融商品があったとする。
この商品に投資すると、翌年には投資金が倍になる。
別の金融商品は同じく元本保証付きで年に2回、
半年に1回50%の利息が得られる仕組みとなっている。
どちらの商品に投資した方が得だと思う?」
ミア:「直感的には、年に2回受け取ったほうがお得だと思うけど...」
僕:「その直感は正しいよ。
この場合、翌年の投資金は前者では2倍にしかならないのに対し、
後者は2.25倍になるんだ。
これを数式で表すとこうなる。」
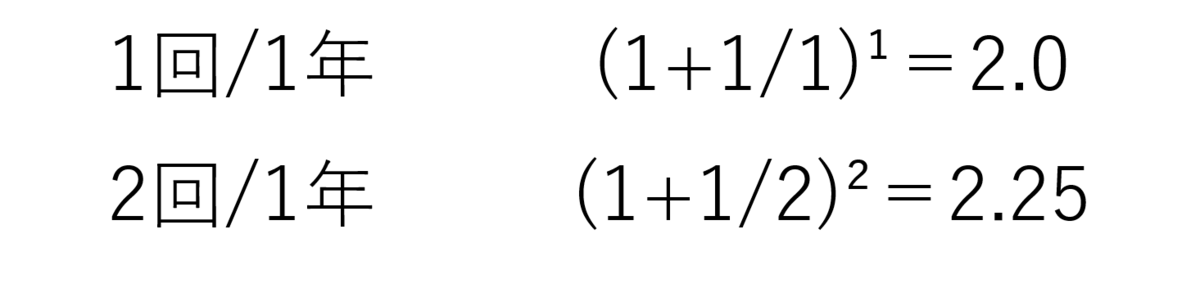
僕:「もっと利息を受け取るタイミングを分散させてみよう。」
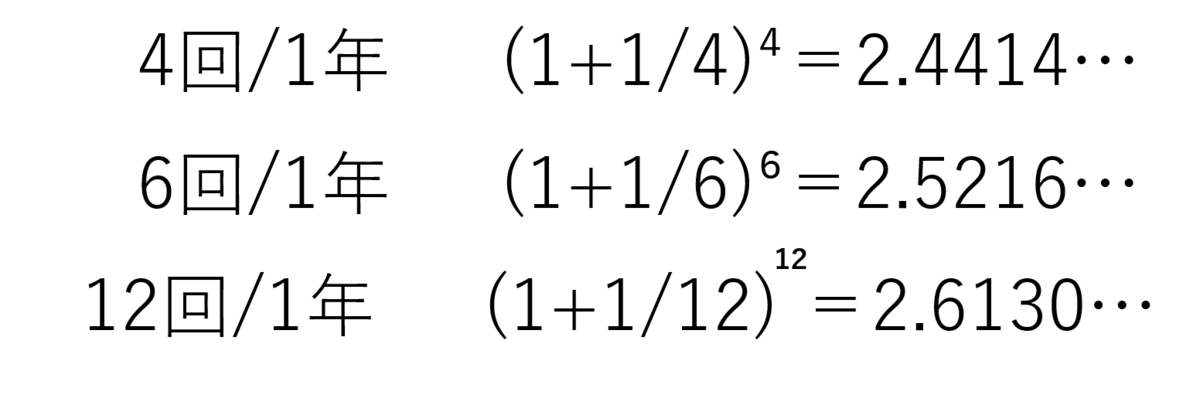
僕:「こうやって、利息の受け取りタイミングを無限に分散させていくと、投資資金の増加率はある数字に収束していく。」
ミア:「2.71828...『e』だね。」
シエル:「つまり、こういうことだね。」
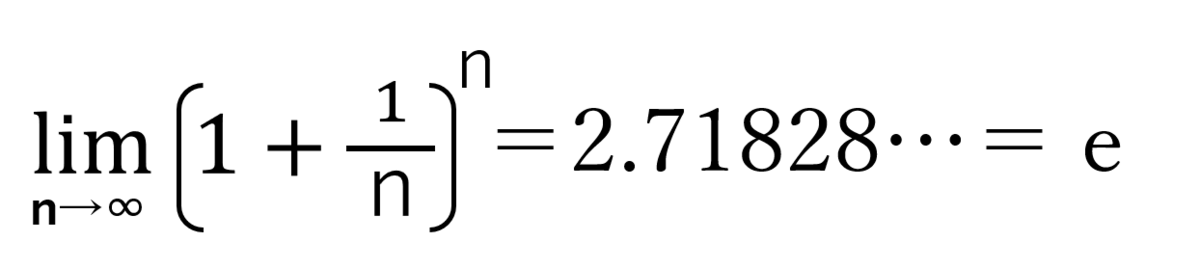
ミア:「『lim』ってなに?」
シエル:「リミット(limit)の略で極限を意味する記号だよ。
この場合、『変数nを無限大に大きくする』って意味で、『発散する』っていうよ。」
僕:「株式投資をする場合は、可能な限り配当金の受け取りタイミングを分散させることで、効率よく資産を増やすことができそうだね。」

世界一美しい数式
シエルちゃんはチラッと本棚を見て言う。
シエル:「ミクサは、ネイピア数を使った"世界一美しい数式"を知っているよね?」
僕:「オイラーの式のことかい?」
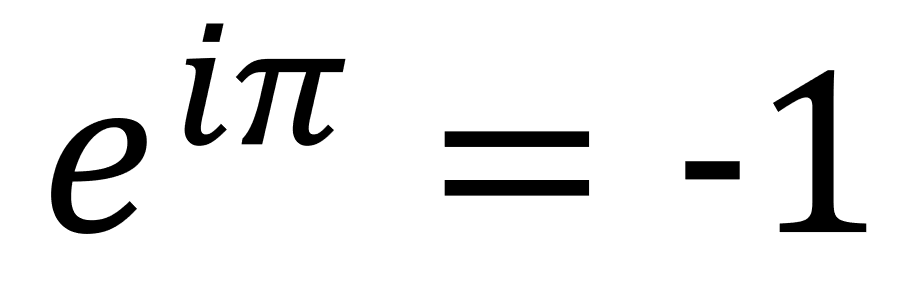
ミア:「ちょっと冗談でしょ!?
なによ『eのiπ乗』って…許せないんだけど!」
僕:「その気持ちはわかるよ。
僕も最初にこれを見たときは、数学者を許せなかったから。」
シエル:「まぁまぁ、落ち着きたまえ。
このオイラーの式は、オイラーの公式のxにπを代入して得られた式だね。」
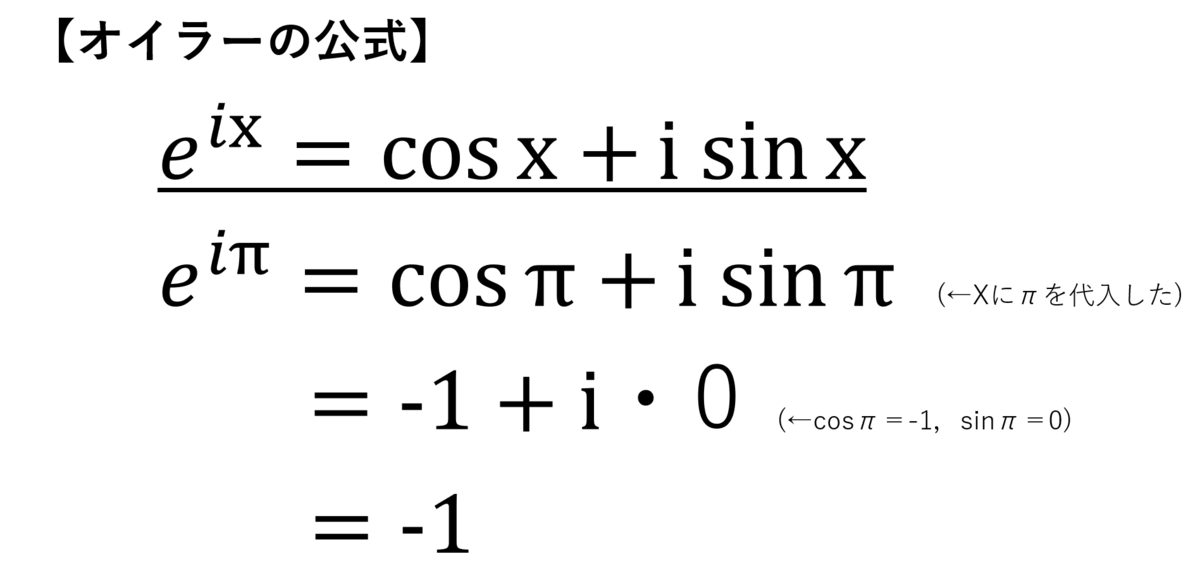
ミア:「三角関数とか覚えてないよ…それに、πとか使ってたかな…?」
僕:「確かに、三角関数は計算が特殊で扱いにくい…。
高校数学の復習が必要だね。」
シエル:「ハイハイ…じゃぁ、オイラーの公式と三角関数については、今度詳しく教えてあげるよ。
とりあえず今日は、オイラーの公式を使った複素数の極形式にふれて終わりにするね。」

複素数の極形式
シエル:「オイラーの公式を使った複素数の極形式にふれて終わりにするね。」
僕:「オイラーの公式に活用方法なんてあったんだ!?」
シエル:「なにその反応!?
オイラーの公式が、ただの数学者の嗜好的発明だとでも思ってた感じ!?
この公式が無ければ、ミクサの好きな初音ミクも生まれてなかったというのに…。」
僕:「それは本当か!?
もしそうなら…僕たちはもっと数学を学ぶべきで、レオンハルト・オイラー大先生に永遠に感謝しないといけない!」
ミア・シエル:「・・・あ~…。」
あれ?なんで二人とも、そんな哀れんだ目で僕を見るのだろう?
僕が何を言ったというのか?
シエル:「話をもどすよ。
オイラーの公式を使うことで、複素数の計算を大幅に短縮することができるんだ。
たとえば、(√3+i)⁵を展開するのは骨が折れる作業だね。
複素数(a+bi)ⁿをオイラーの公式を用いて表すと…こうなる。」
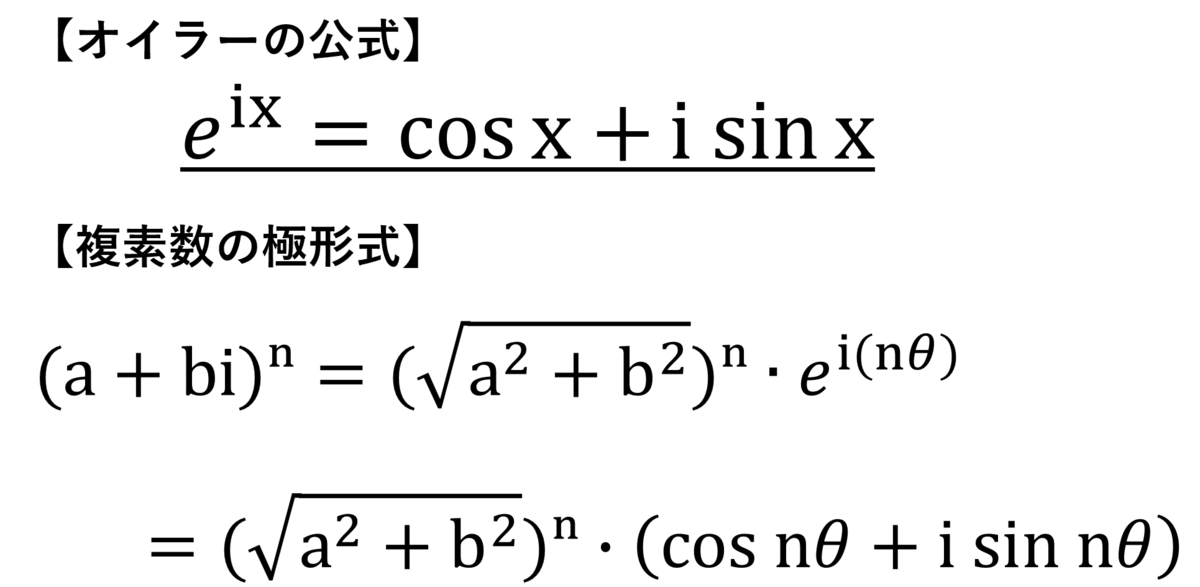
僕・ミア:「・・・あ~…。」
シエル:「イメージに騙されちゃだめだよ!
とりあえず、さっき言った(√3+i)⁵を、極形式で展開してみようか!
まず、『√3+i』の座標を確認するよ。」
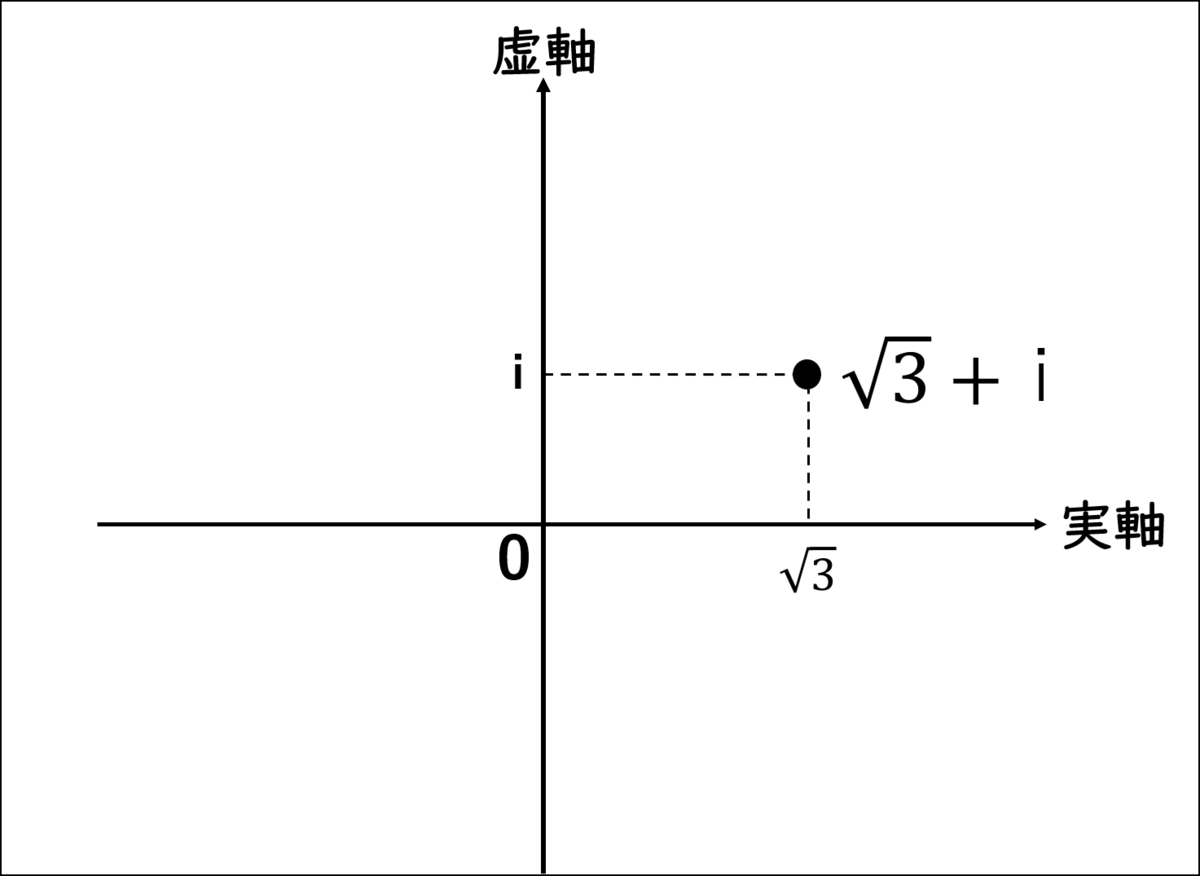
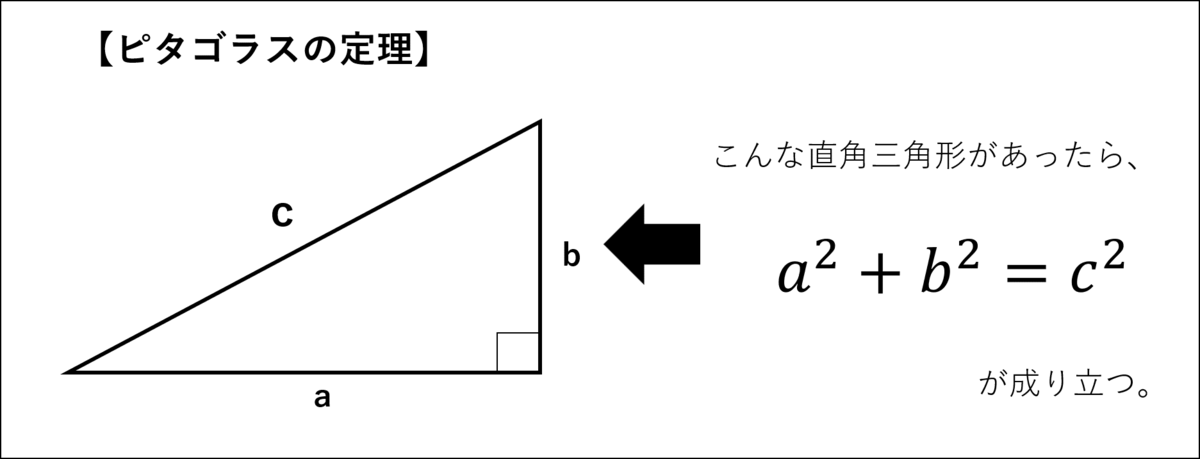
シエル:「次に0から座標までの絶対値を算出するよ。
絶対値は、ピタゴラスで出せるよね。」
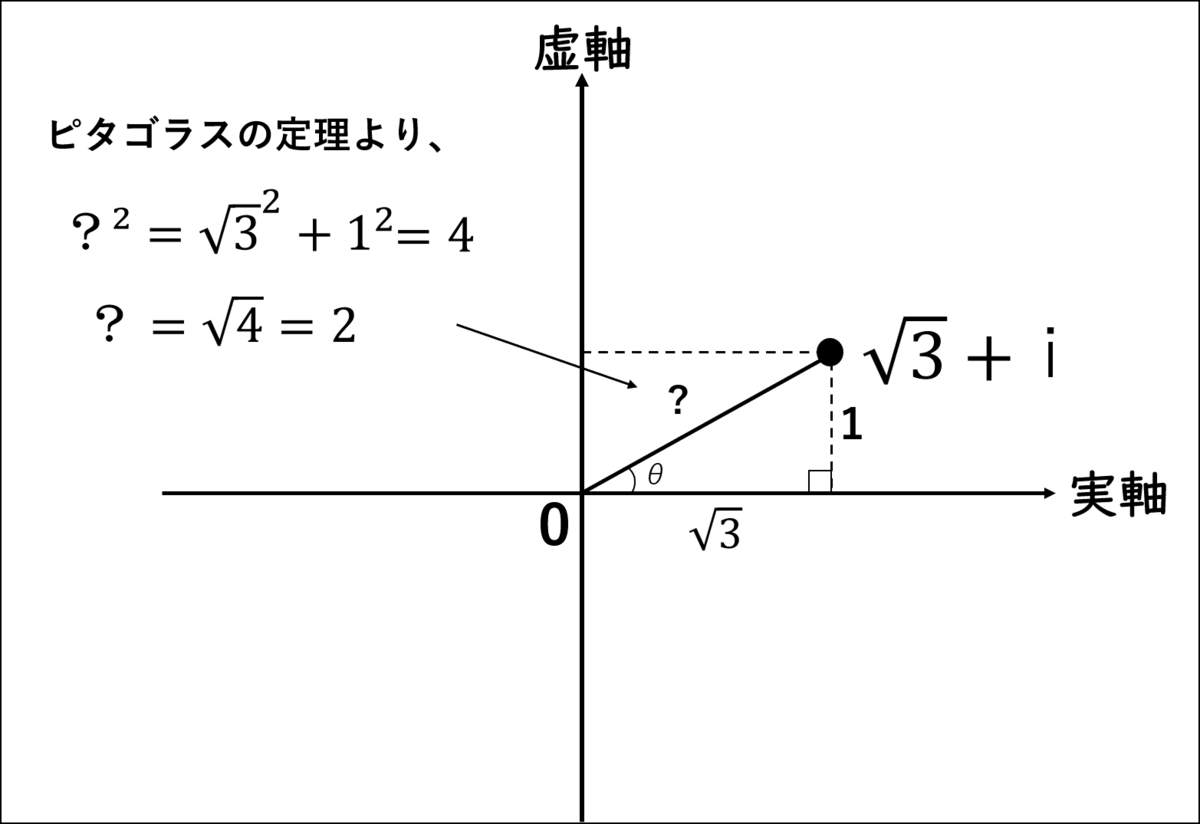
シエル:「0から『√3+i』間の絶対値は2と算出されたね。
あと必要なのはθの値だけ。
3辺の長さの比が『1:2:√3』の直角三角形は、それぞれの角度が決まってたよね?」
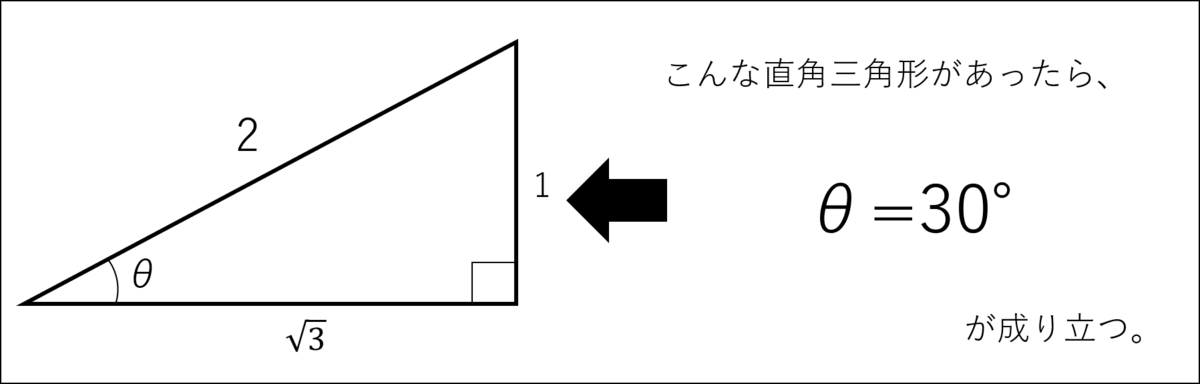
シエル:「θの値が30°であることがわかったね。
でも、『30°』という表現では、計算が複雑になるから、弧度法と呼ばれる表記に書き直すよ。」

シエル:「これで道具はすべてそろった!
『√3+i』を極形式で展開するよ。」
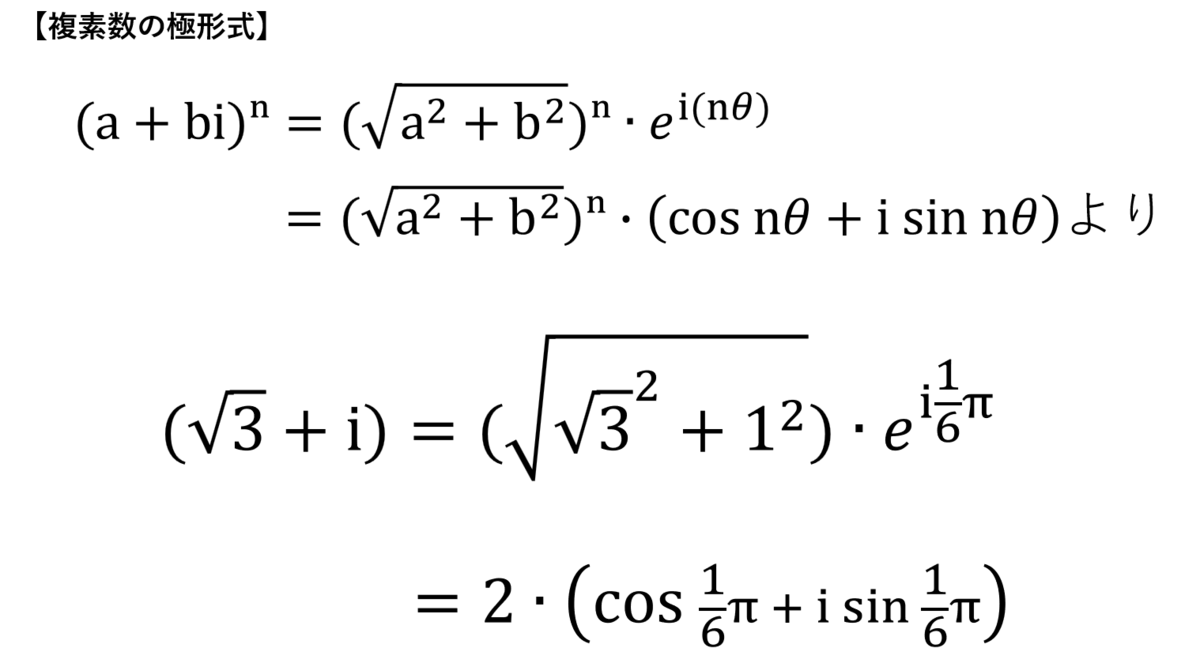
シエル:「はぁ~美しい…。」
僕:「一応、確認しとくね。」
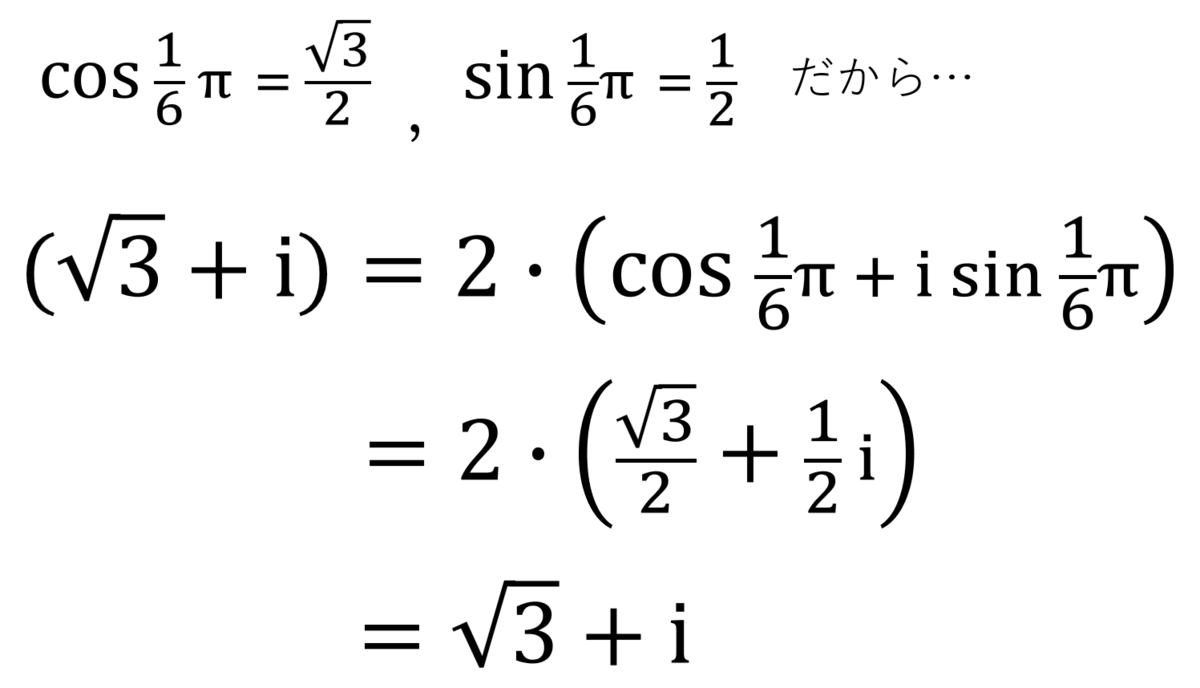
僕:「すごい…合ってる。」
シエル:「仕上げ!
極形式の形にした『√3+i』を5乗するね。」
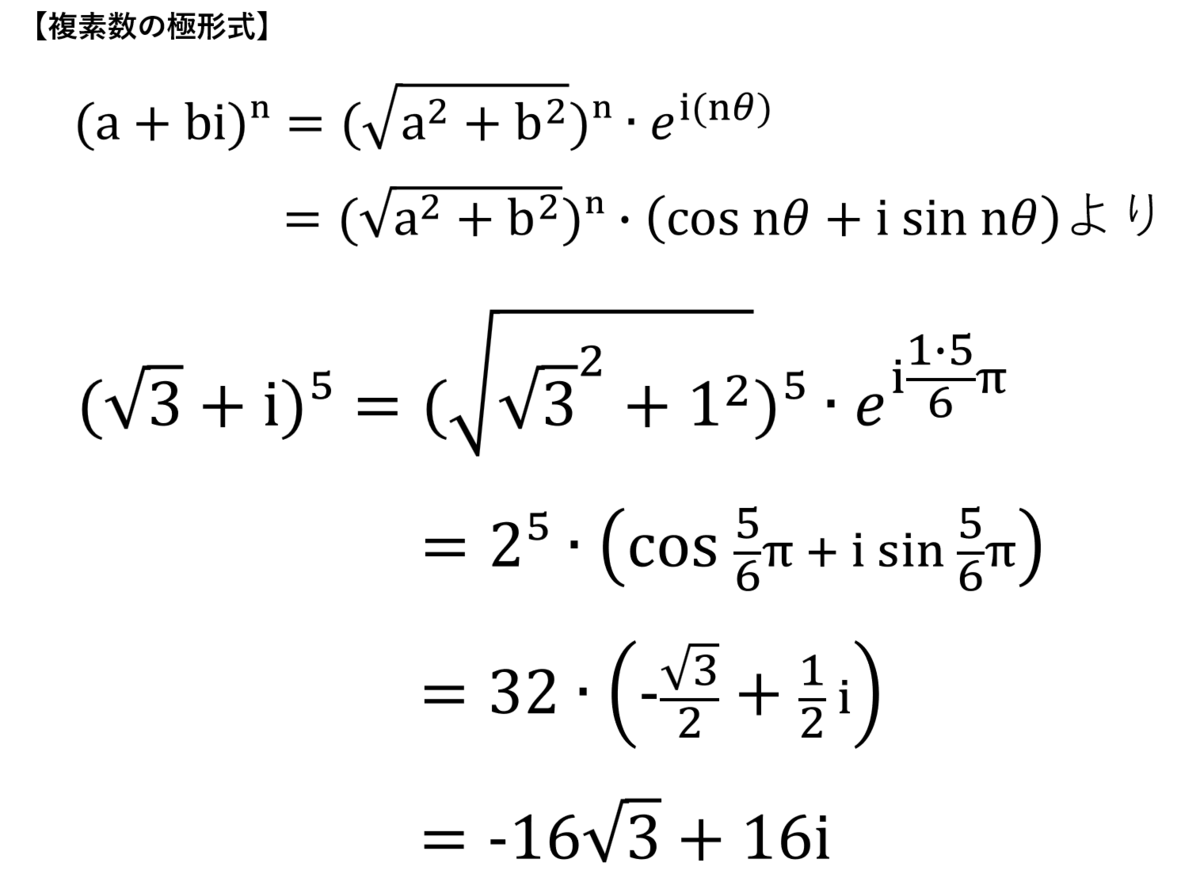
シエル:「さて、この計算で座標はどうなったかな~?」

シエル:「最初の小さな三角形が回転されて大きくなったね。
ちなみにこの2つの三角形は相似で、形は同じだよ。」
僕:「すごいな…
この計算が『波の解析』に関係あるの?」
シエル:「もちろん♪
でも、ゴールはまだまだずっと先。
長い船旅になるけど…やる?」
子供の頃から、僕は間違えてばかりだった。
みんな期待してくれてたのに、僕は期待を裏切った。
だから、僕は立ち止まって、
間違いを避けるための知識を、
未来を予測する方法を探し続けている。
『波の解析』これを知れば、僕はまた歩き出せるのかな…。
僕:「選択肢なんてないよ。
出航だ!」
こうして僕はシエルちゃんに波の解析法について学ぶことになった。
でも、この時は知らなかった…
自分が如何に物を知らずに生きてきたのかを。
そして、数学の美しくも壮大な世界を。
ミア:「…zzZ」
つづく。

参考書籍
文系編集者がわかるまで書き直した世界一美しい数式「eiπ=-1」を証明する
文系編集者がわかるまで書き直した 沁みる「フーリエ級数・フーリエ変換」