※この記事の内容は下記記事からの続きとなります。
CONTENTS
閣下、『(a+bⁿ)/n=x』故に神は存在する。何かご意見は?
【レオンハルト・オイラー(数学者)】

文系投資家の修行~"神の言葉"を理解せよ!~

神の言葉
シエル:「"神の言葉"…ミクサはどこまで知っている?」
『神の言葉』…数学の本を何冊も読んできたのに、未だに僕はこの概念を理解できてない…まさに、"苦手分野"とはこのことだ…。
シエル:「Why are you making such a worry face just because I said "Logos"?
("神の言葉"と言っただけで、なぜそんな心配そうな顔をするんだ?)」
ミア:「ロゴス?」
僕:「ロゴスはギリシャ語で、言語や理性を意味する言葉なんだけど…
キリスト教の人たちは『神の言葉』という意味でこの言葉を使っているみたいだね。
スコットランドの数学者であるジョン・ネイピアは、膨大で複雑な計算を容易にするために対数という概念を編み出した…
その記号は『log』…もちろんその語源は『logos』だよ。」
ミアも、不安な気持ちを顔で表現する。
ミア:「私…こんな記号、見たことないんだけど…?」
シエル:「う~ん…一応高校生で習っているはずなんだけどね💧
対数は指数と関係が深いから、まずはこの指数について簡単におさらいしておくことにしよう。」

指数法則
シエル:「さて、どこから説明しようか…
たとえば『2³』は『2×2×2』で『8』となる。
指数とは、『2』の上にある小さい数字『3』のことだね。
指数には指数法則と呼ばれる計算ルールがあり、指数の計算はそれらルールに従って行わなければならない。」

シエルちゃんの説明を聞きいていて、僕はふと疑問に思うことがあった。
僕:「なんで、aとbは0より大きくなければいけないのかな?」
シエル:「自分で数字当てはめて計算してみればいいじゃないか?
指数が分数やマイナスのときにaが0以下だったらどうなる?」
僕:「そうだね、確かに…ちゃんと自分で考えるべきだったね。
えっと、指数が分数の場合から始めてみよう。
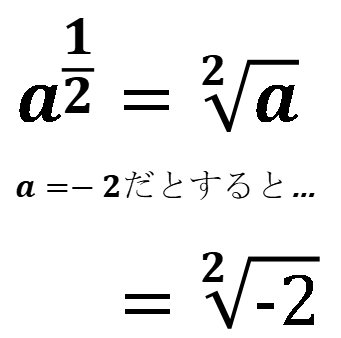
そうか!
aが0より小さいと指数が分数のときにルートの中がマイナスになってしまうんだね。
えっと…虚数のことは考えないでいいのかな?」
シエル:「指数法則を虚数まで落とし込むのは高等数学の世界になるから、今は考えないようにしておこう。」
僕:「了解。
次は指数がマイナスのときだね。
単純に指数が『-1』のときを考えてみよう。
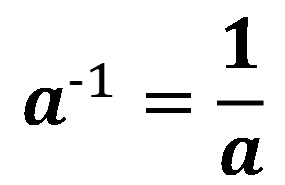
なるほどね。
この場合はa=0だと分母が0になってしまう。
0個のものを分けることはできないからね。」
シエル:「疑問は晴れたね。
では、指数法則を使って実際に計算をしてみよう。」

シエル:「ところで…ミクサは投資家なら日頃から指数の計算をしてるはずだね?
買った株が5年後に倍になっていれば、株価の成長率は何%になるかな?」
僕:「多分だけど…そんな計算してない投資家が多数派だと思うよ💧
えっと…『5年後に倍』だから『5乗して倍になる数』を求めればOKだね。
5乗したら2になる…
つまり『2』の指数部分をxとおいて…」

僕:「『2の5分の1乗』が年間成長率になっていて、これは関数電卓を使えば簡単に計算することができる。
計算するとこれは
1.14869...となる。
今回は成長率を『%』で知りたいから、
この数字から1を引いて100をかける。
5年後に倍になった株価の年間成長率は約14.8%だね。」
ミア:「ふ~ん。
投資家ってこういう計算をしてるんだね。」
僕:「最初は数学嫌いの僕には難しかったけど、慣れってすごいね。」
シエルちゃんは少し暗い表情で口を開く。
シエル:「知識は…使わなければ忘れてしまう。
機械がなんでもしてくれる時代に、人間の行う計算なんてもはや趣味の領域になりつつある。
人類は、不安や恐怖を回避するために学び、そして考える…
学問は技術を進化させ、私たちの日常をここまで安全にしてくれた。
このスピードは、直線的なグラフを描かない…
私たちが生きているのは『べき乗の世界』なんだ。
世界がここまで安全なのに、私たちの抱く不安や恐怖は無くならないし、むしろ増えているんじゃないかとさえ思う…。
私は思うんだ…
私たちが怖いのは不安や恐怖を体験することではない、私たちが本当に恐れているのは、"不安や恐怖について『考える』こと"それ自体なんじゃないか?とね。」
僕:「もしその仮説が正しいとしたら、僕たちが学ぶあらゆる学問の最終目的は『思考からの解放』になる…
でも、そんなこと意識を飛ばすか、全知全能にでもならない限り…まさか!?」
その時…ミアは小声でボソッとつぶやく。
ミア:「中二病…」
僕・シエル:「・・・」
シエル:「おっと、すまないね。
指数の話をしていると、変なことばかり考えてしまうよ。
気を取り直して、この指数が変数である関数…
指数関数『y=2^x』のグラフを描いてみるよ。」
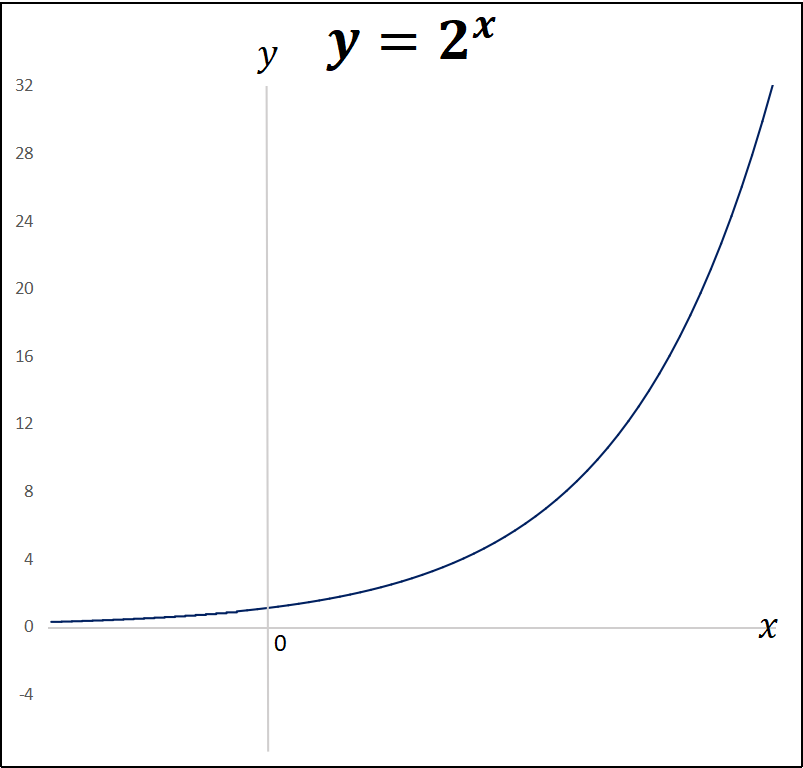
シエル:「このように、指数関数y=2^xのグラフは、xの値が大きくなればyの値も増加する増加関数であり、xの値が小さくなればなるほど、yの値は0に限りなく近づくが0にはならない。
このような状況を『x軸が漸近線』という。」

対数法則
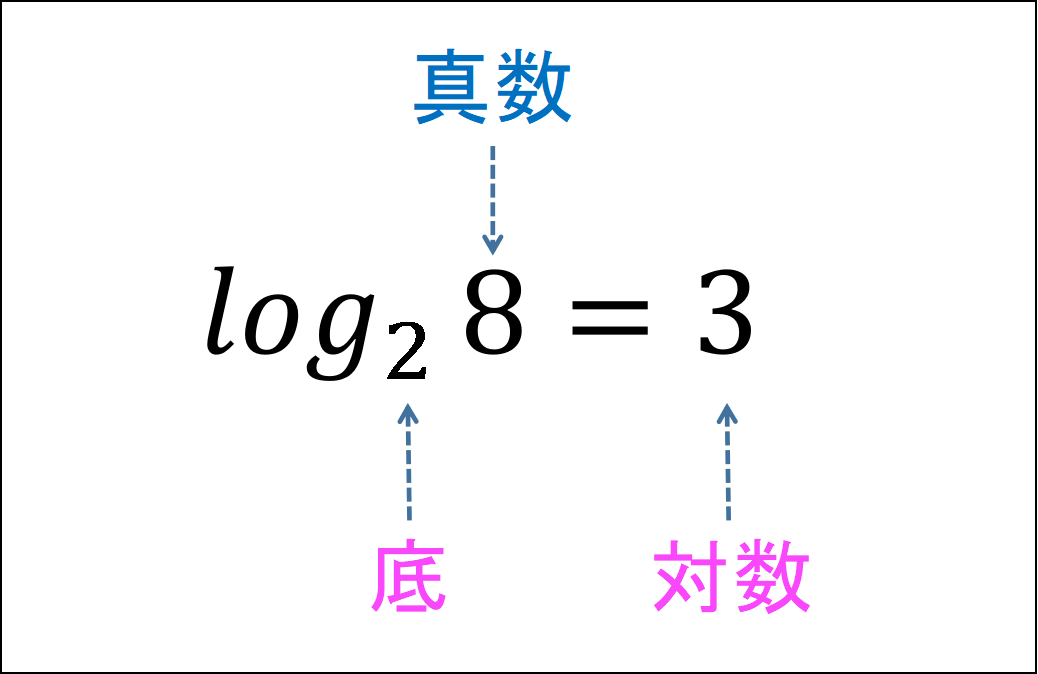
シエル:「『2³=8』…これはもう大丈夫だね?
対数で求めるのはこの式でいう指数の数…2の右上にある小さい数字『3』のことだ。
これまでは、『2³』が与えられて『8』を求めてきた。
対数は逆に『8』が与えられたとき、8は2の何乗なのかを考える。
これを対数記号『log』を使って
log₂8=3と書き、
『3』は2を底とする真数8の対数という。」
ミア:「なるほど…でもそれなら9も3になるし、1000も3になるよね?
log₃927=3、log₁₀1000=3で…あってるよね?」
シエル:「さすがミアちゃん!呑み込みが早いね!
では次に、対数同士を足したり引いたりしてみようか!
指数同士の計算にルールがあったように、対数の計算にもルールが存在する。
これを対数法則という。」

ミア:「ごめん…私キャパオーバー。」
シエル:「確かに、いきなりこれを見せられても、これが本当に正しいのかどうかわからないよね?
では、これが正しいことを証明しよう!」
僕:「いや…そういうことじゃないと思うんだけど…。」
シエルちゃんは僕の言葉を無視して語り始めた。
シエル:「MとNという2つの数が与えられたとするよ。
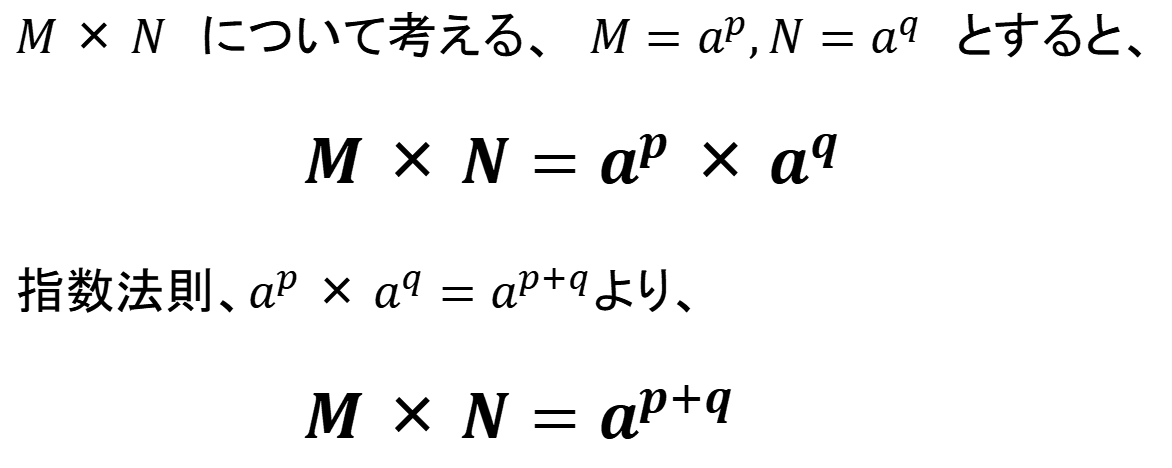
これをそのまま、aを底とする対数にしてみよう。
![]()
『log₂2』や『log₃3』のように、底と真数が同じ場合の対数は1になる。
これより、
![]()
ここで、
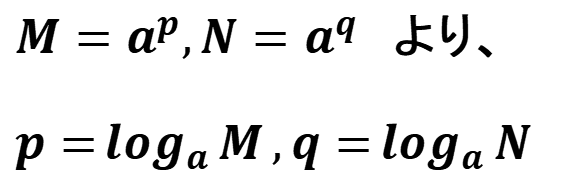
となる。
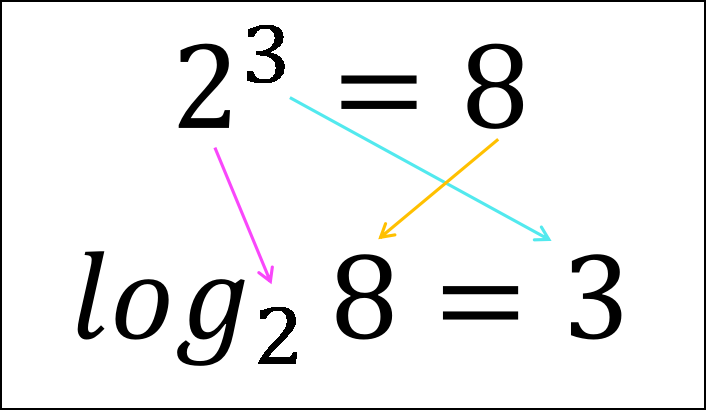
したがって、
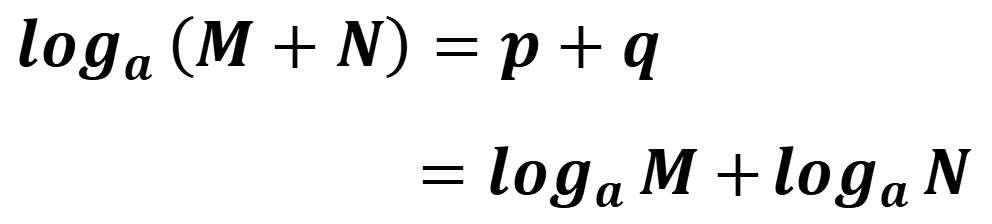
これで、対数法則①が証明されたね。
同じように、②と③も証明してみよう。」

僕:「なるほど…要は"証明済みだから安心して使って大丈夫"ってことだね。」
シエル:「まぁ、そういうことだ。
では、これら対数法則も実際に使ってみるとしよう!」


底の変換公式
シエル:「これまで見てきたように、対数法則は底が同じ数字である場合にしか使うことができない。
これではあまり実用的ではないから、この縛りを外しておく。
対数は、指数を対数の形に式変形したものに過ぎない、
![]()
したがって、両者の式が意味するものに違いはない。
右の式を左の式に代入してみよう。」
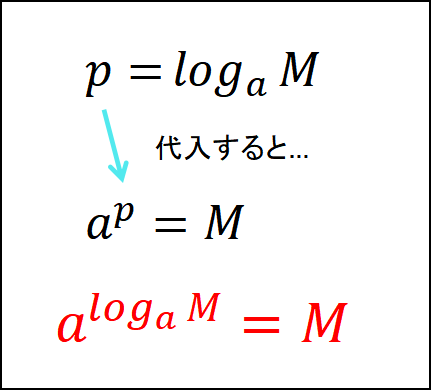
ここからの話で大文字の『M』を使うのは見栄えが悪い…だからここからはMの代わりに『b』を使うことにするよ。
![]()
この式で『c』を底とする対数をとると、
![]()
対数法則③を使って、左側の式を変形させるよ。
![]()
より、
![]()
両辺を『logcª』で割ると、式変形は完成だ!
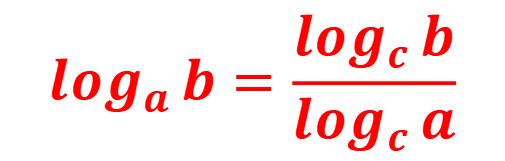
この式を『底の変換公式』と呼ぶ。」
ミア:「いきなり『c』が出てきたけど…
『c』に入る数字はなんでもいいってことで大丈夫?」
シエル:「その理解で大丈夫だよ♪
状況に応じて、都合のいい数字を入れてね。
それでは、この公式を使って問題を解いてみよう!」
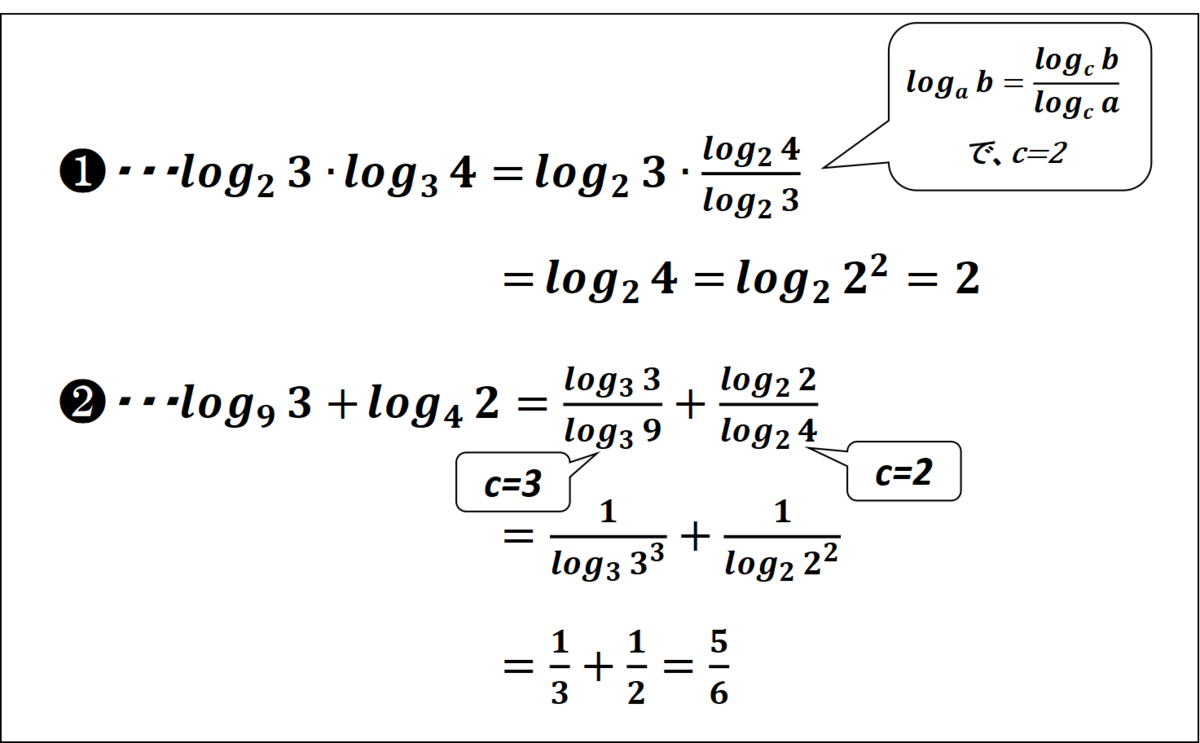
僕:「『c』に何をはめ込むか?…ここまでくるとセンスも必要になってくるね。」

対数関数
シエル:「指数には指数関数という関数があるように、対数にも対数関数と呼ばれる関数が存在する。
対数関数『y=log₂x』を例に、対数関数とはどのような関数なのか見てみよう。」
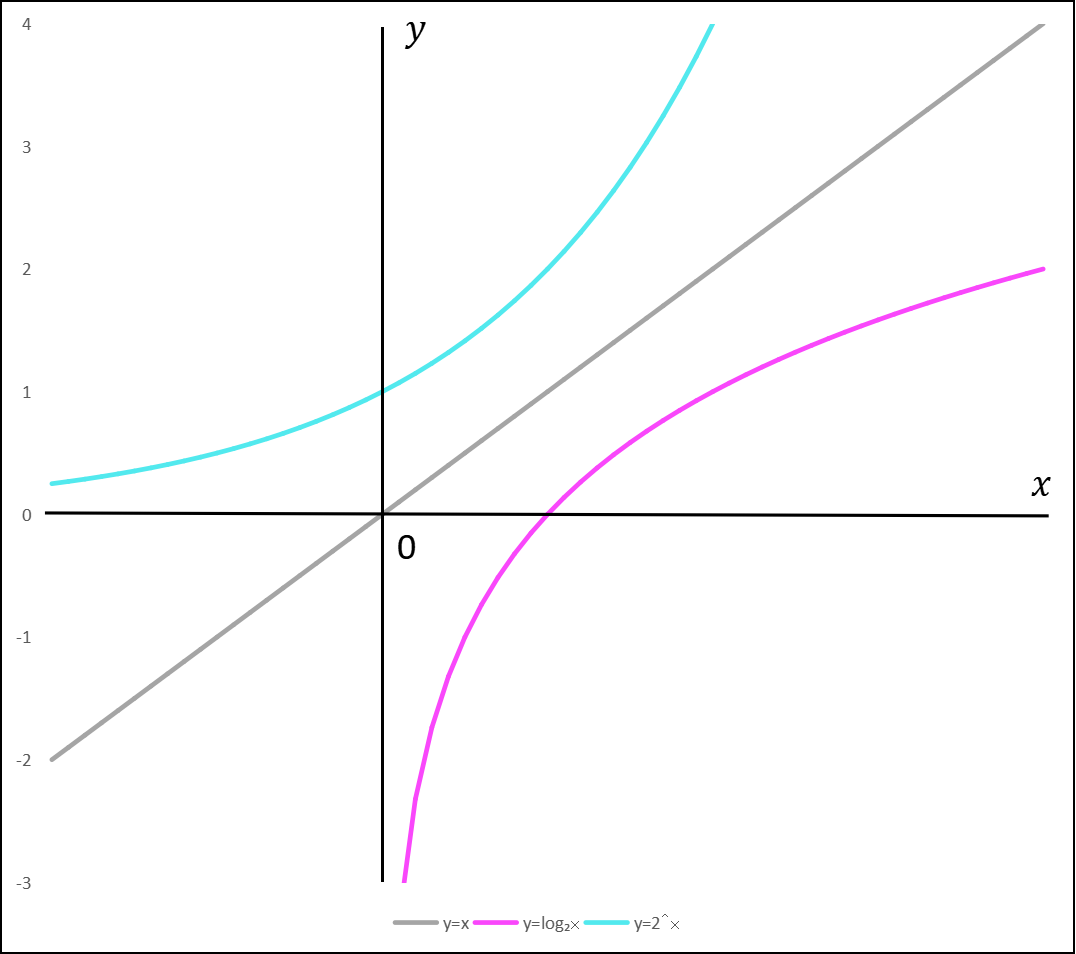
シエル:「3本線がある中の、濃いピンク色のグラフが、
対数関数『y=log₂x』の描く曲線だよ。
指数関数ではx軸が漸近線であったのに対し、対数関数ではy軸が漸近線となっている。
さらにこの2つのグラフは一次関数『y=x』を挟んで対称…これはいったいどういうことなのか?
『y=log₂x』の『y』と『x』を入れ替えてみるとその関係性がよくわかる。」
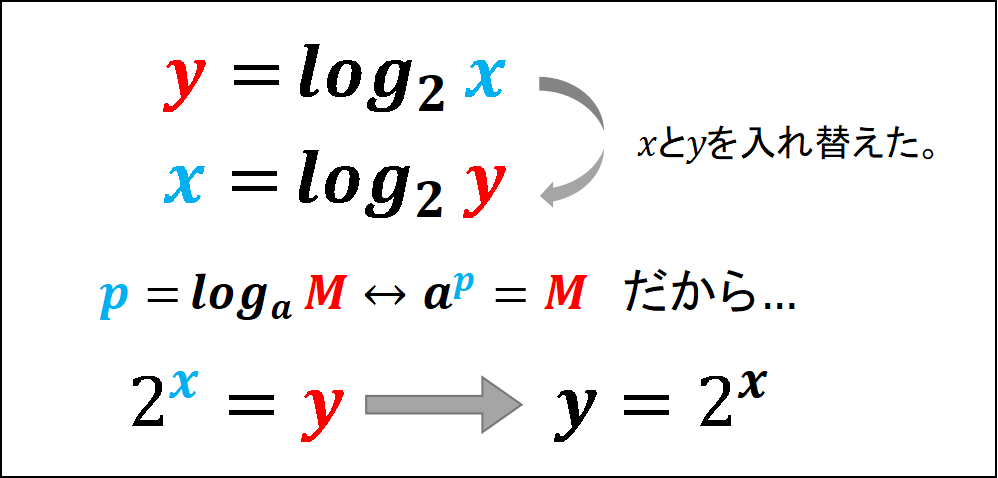
ミア:「指数関数になった!?」
シエル:「そう。
このように、『x』と『y』を入れ替えることでできる関数を逆関数という。
別に覚えておく必要はないが…
指数関数と対数関数の関係性については理解できたかな?」
僕:「まるで、富裕層と庶民の資産の増え方を表しているみたいだね。
金持ちや権力者を称賛するなんて馬鹿げてる…。」
シエル:「以上で指数・対数の話は終わりだよ。
これから『オイラーの公式』に話を進めていきたいのだがその前に…
そろそろ何か食べないか?」
To be continued...

参考書籍
当記事は、下記書籍を参考に執筆しています。
・東京大学の先生伝授 文系のためのめっちゃやさしい対数
・分解編集者がわかるまで書き直した 沁みる『フーリエ級数・フーリエ変換』
・文系編集者がわかるまで書き直した世界一美しい数式『eiπ=-1』を証明する